Предмет: Алгебра,
автор: paxamvd1992
Найти производные данных функций:
Приложения:
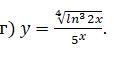
Ответы
Автор ответа:
0
Ответ:
=============================
Объяснение:
Приложения:

Автор ответа:
0
Ответ:
Объяснение:
Сложная функция вида:
Тогда производная будет выглядеть следующим образом:
Преобразуем:
Похожие вопросы
Предмет: Алгебра,
автор: ludmilavlasuk556
Предмет: Українська мова,
автор: nevmivakoartem
Предмет: Математика,
автор: gassgafferd
Предмет: Математика,
автор: лиза11114
Предмет: Математика,
автор: dimabahtin99