Предмет: Геометрия,
автор: wiwwo
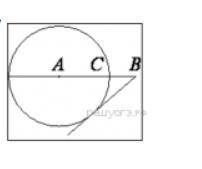
На отрезке AB выбрана точка C так, что AC=60 и BC=5 . Построена окружность с центром , проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности
Приложения:
Ответы
Автор ответа:
24
Ответ:
25 ед. изм.
Объяснение:
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть.
ВМ - секущая, равная 2АС+ВС, т.к. проходит через центр окружности; ВМ=АС+АМ+ВС=60+60+5=125
ВК²=ВМ*ВС=125*5=625; ВК=√625=25 ед. изм.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: UvUwU
Предмет: Литература,
автор: Igor32135
Предмет: Қазақ тiлi,
автор: akhmetovaalina77
Предмет: Химия,
автор: michaszek616