Предмет: Физика,
автор: chausovnikitka
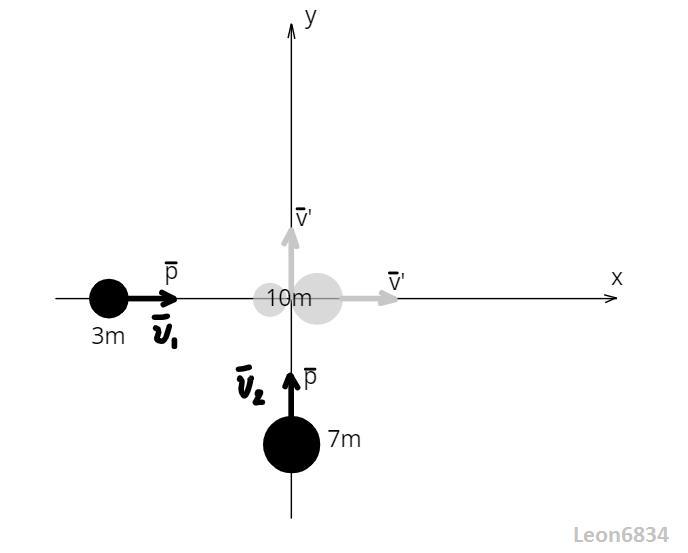
По гладкой горизонтальной поверхности стола по двум взаимно перпендикулярным направлениям двигались два шарика массами 3m и 7m. Величины импульсов этих двух шариков были равны. После удара они слиплись и начали двигаться как одно целое. Какая часть начальной кинетической энергии шариков перешла в теплоту? Ответ выразить в процентах, округлив до целых.
Ответы
Автор ответа:
3
Дано:
m₁=3m;
m₂=7m;
p₁=p₂=p;
________
Найти
Решение:
Так как импульсы тел равны, можно записать:
Распишем закон сохранения импульса в проекциях на координатные оси:
Хорошо видно, что после соударения тела буду двигаться с равными проекциями скоростей.
Результирующая скорость:
Первоначальное значение кинетической энергии обоих тел:
Конечное значение кинетической энергии после взаимодействия:
Перешла в теплоту:
Процентное соотношение:
или 58%
Ответ: 58%.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kakashihasace
Предмет: Математика,
автор: comcomturatbekovaajy
Предмет: История,
автор: asapalcik
Предмет: Математика,
автор: haydro
Предмет: Математика,
автор: vadum081