Предмет: Алгебра,
автор: HELP12345678900000
ЗАДАНИЕ
Решите уровнения
Приложения:
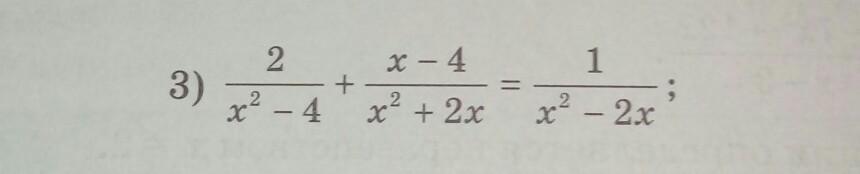
Ответы
Автор ответа:
1
Ответ: x = 3 (так как х = 2) не допускается по ОДЗ.
oganesbagoyan:
Ответ: x =3. * * * x = 2 посторонний корень * * *
ОГРОМНОЕ СПАСИБО
Автор ответа:
2
Ответ: x =3.
Решение :
2/(x-2)(x+2) +(x-4)/x(x+2) = 1 /x(x-2) * * * ОДЗ : x ≠ 0 ; ±2
2x +(x -4)(x-2) =x+2⇔2x + x² - 6x +8 = x+2 ⇔x² -5x +6 = 0;
x₁ = 2 ; x₂=3 . Но x₁ = 2 ∉ ОДЗ .
Ответ: x =x₂ =3.
ОГРОМНОЕ СПАСИБО
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: МХК,
автор: kittyqxl
Предмет: Алгебра,
автор: akkawae
Предмет: Геометрия,
автор: vipvinxop
Предмет: Математика,
автор: ermak211