Предмет: Алгебра,
автор: Huql
Решите. Заранее спасибо
Приложения:
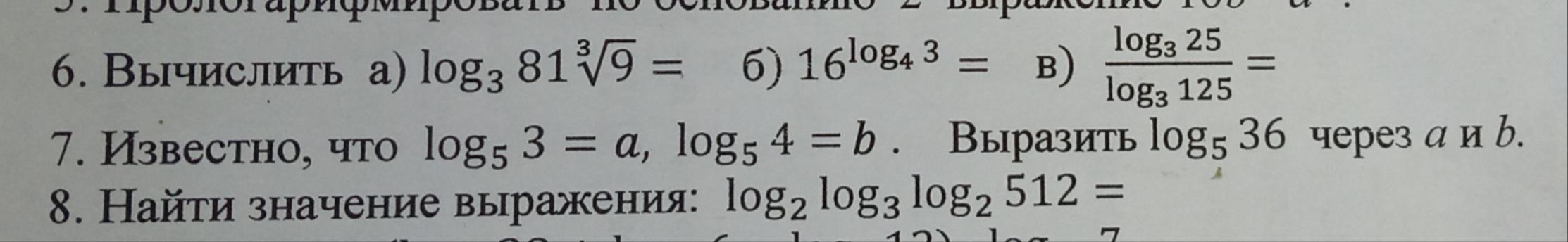
Ответы
Автор ответа:
0
Ответ:
решение на фотографии
Приложения:
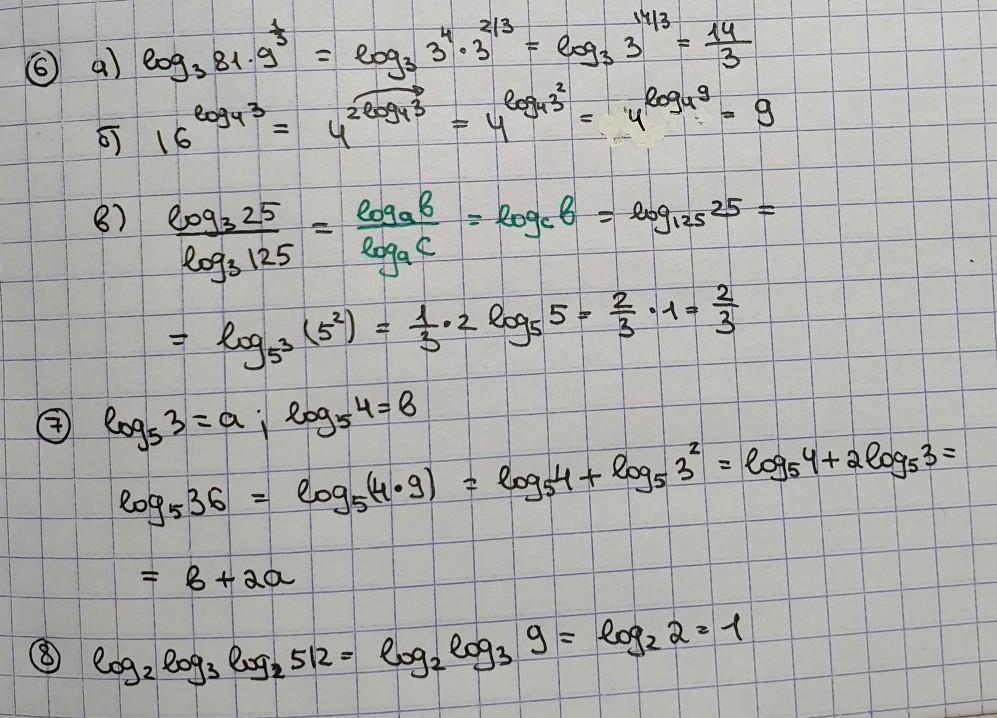
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: anime777777
Предмет: Алгебра,
автор: nastazimina91
Предмет: История,
автор: Katsumii
Предмет: Математика,
автор: аноним270
Предмет: История,
автор: Амиго111111