Предмет: Алгебра,
автор: statkevichelenka
Найдите сумму корней уравнения на промежутке [-п, 2п]
Приложения:
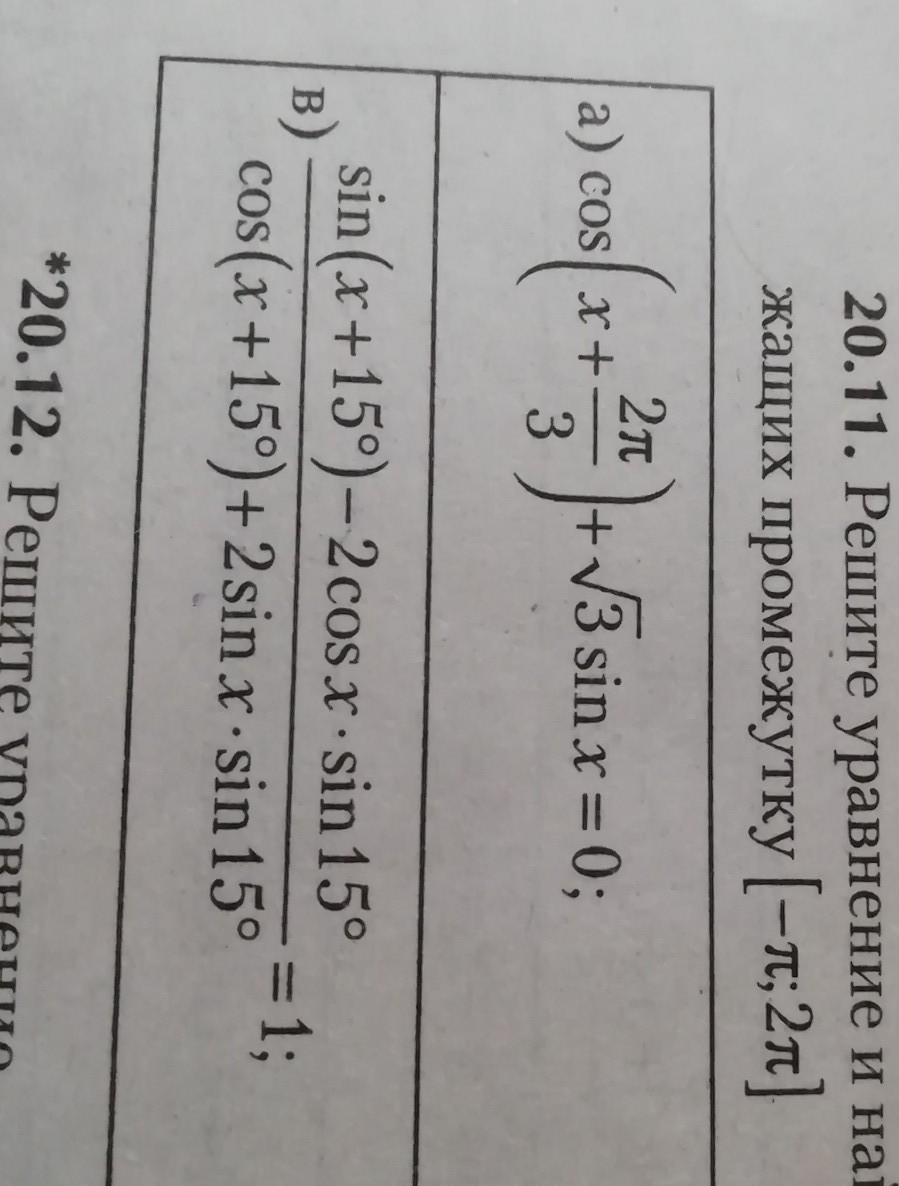
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: pers0kv
Предмет: Қазақ тiлi,
автор: sajmuhanovak
Предмет: Биология,
автор: anyadtt
Предмет: Математика,
автор: ramazaolga
Предмет: Литература,
автор: Hoooba228