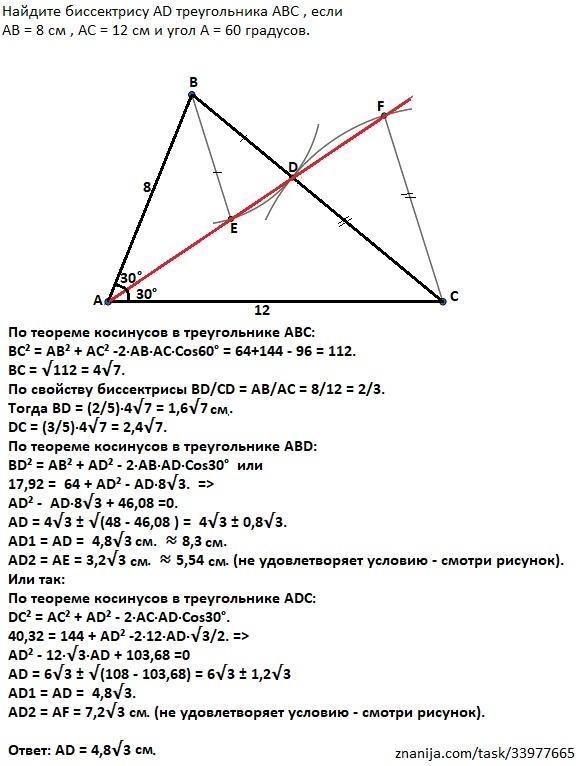
Найдите биссектрису AD треугольника ABC , если AB = 8 см , AC = 12 см и угол A = 60 градусов
Ответы
Ответ:
AD = 4,8√3 ед. ≈ 8,3 см.
Объяснение:
Дано: АВ=8, АС=12, ∠ВАС = 60° , AD - биссектриса.
По теореме косинусов в треугольнике АВС:
ВС² = АВ² + АС² -2·АВ·АС·Cos60° = 64+144 - 96 = 112.
ВС = √112 = 4√7.
По свойству биссектрисы BD/CD = AB/AC = 8/12 = 2/3.
Тогда BD = (2/5)·4√7 = 1,6√7 см.
DC = (3/5)·4√7 = 2,4√7.
По теореме косинусов в треугольнике АВD:
ВD² = АВ² + АD² - 2·АВ·АD·Cos30° или
17,92 = 64 + АD² - AD·8√3. =>
АD² - AD·8√3 + 46,08 =0.
AD = 4√3 ± √(48 - 46,08 ) = 4√3 ± 0,8√3.
AD1 = AD = 4,8√3 см. ≈ 8,3 см.
AD2 = AE = 3,2√3 см. ≈ 5,54 см. (не удовлетворяет условию - смотри рисунок).
Или так:
По теореме косинусов в треугольнике АDС:
DС² = АC² + АD² - 2·АC·АD·Cos30°.
40,32 = 144 + АD² -2·12·АD·√3/2. =>
АD² - 12·√3·АD + 103,68 =0
AD = 6√3 ± √(108 - 103,68) = 6√3 ± 1,2√3
AD1 = AD = 4,8√3 см.
AD2 = AF = 7,2√3 см. (не удовлетворяет условию - смотри рисунок).
P.S. Есть формула для биссектрисы треугольника:
L = √(a*b-e*d) (a и b - стороны угла; e и d - отрезки стороны с).
В нашем случае a = 8, b = 12, e = 1,6√7, d = 2,4√7. Тогда:
L = √(96-26,88) = √69,12 = 4,8√3 см.