Предмет: Алгебра,
автор: BoxTears
Привести уравнения линий к каноническому виду.
Помогите, пожалуйста, нужно подробное решение, ломаю голову сижу :(((
Приложения:
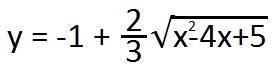
Ответы
Автор ответа:
0
Дана функция
Начнём с выражения под корнем.
Минимум по производной равен: 2х - 4 = 0, х = 2.
Под корнем 4 - 4*2 + 5 = 1.
Минимум всей функции равен -1 +(2/3)*1 = -1/3.
Перенесём -1 влево и возведём обе части уравнения в квадрат.
(у + 1)² = (4/9)(x² - 4x + 5).
В правой части выделим полный квадрат.
x² - 4x + 5 = (x² - 4x + 4) - 4 + 5 = (x - 2)² + 1.
Правая часть примет вид (4/9)((x - 2)² + 1) = (4/9)(x - 2)² + (4/9).
Перенесём квадрат с х влево:
(у + 1)² - (4/9)(x - 2)² = 4/9.
Разделим обе части на 4/9.
((у + 1)²)/(4/9) - ((x - 2)²/1) = 1.
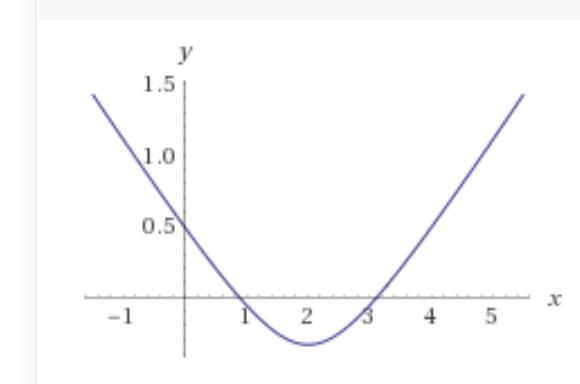
Получили уравнение гиперболы, повёрнутой на 90 градусов.
Но в соответствии с заданием, только верхняя часть этой гиперболы удовлетворяет заданному уравнению.
Приложения:
BoxTears:
О боже, спасибо большое)))
Похожие вопросы
Предмет: Қазақ тiлi,
автор: goi5bgd
Предмет: История,
автор: ursulenkosvetlana9
Предмет: Математика,
автор: martalibini
Предмет: Математика,
автор: Sonyabintik
Предмет: Геометрия,
автор: vitaly100174