Предмет: Алгебра,
автор: ayiskhan17
ЛУЧШИЙ ОТВЕТ ПОЛУЧАЕТ 45 баллов
----------------------------------------------
с решениями
Приложения:
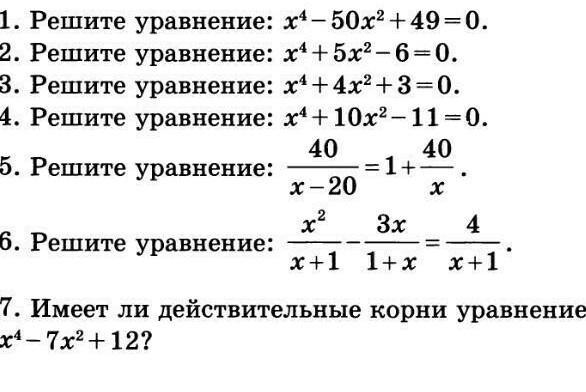
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Уравнение имеет действительные корни.
Похожие вопросы
Предмет: Алгебра,
автор: errornoth
Предмет: Русский язык,
автор: aruzans052
Предмет: Математика,
автор: Dedneznat
Предмет: Физика,
автор: tanichka1999