Question

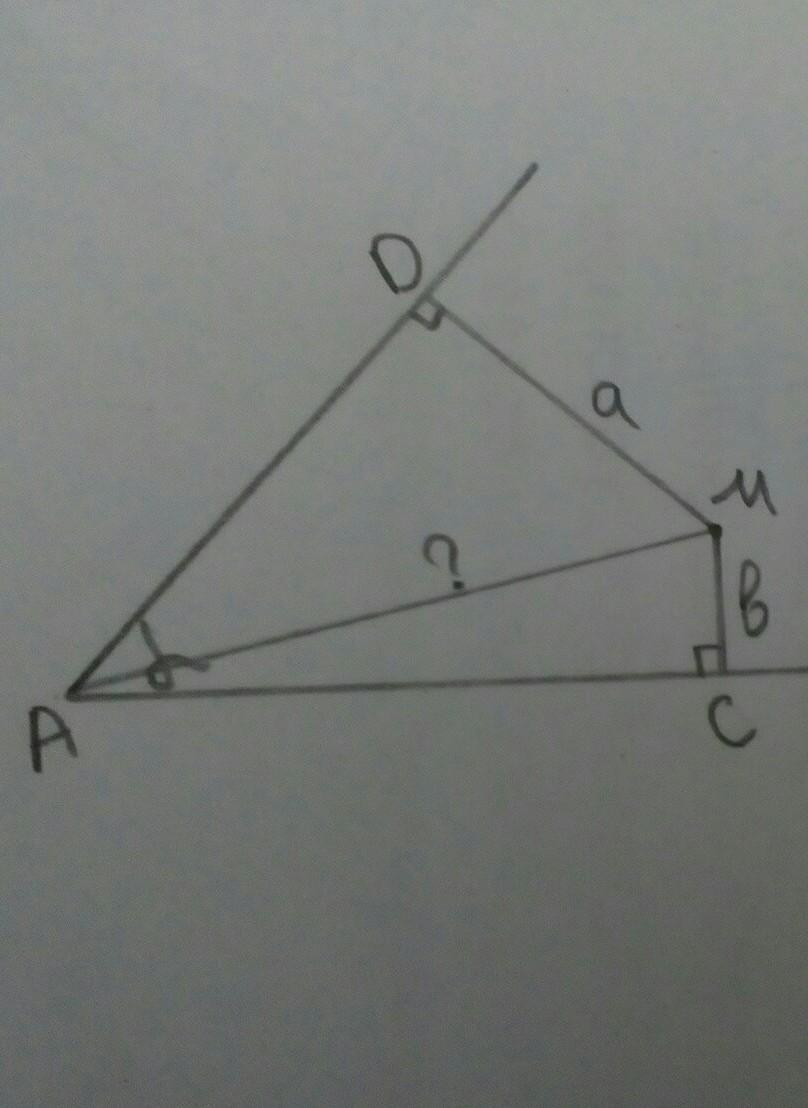
Дан угол А,равный альфа
внутри него лежит точка М
Расстояние до сторон угла равно а и в
Найти: АМ​

Answer 1

Пусть угол против стороны b равен

$\beta$

тогда выразим AM из прямоугольных треугольников ACM и ADM:

$am = \frac{b}{ \sin( \beta ) } \\ am = \frac{a}{ \sin( \alpha - \beta ) }$

приравняем и получим уравнение:

$\frac{b}{ \sin( \beta ) } = \frac{a}{ \sin( \alpha - \beta ) } \\ b \sin( \alpha - \beta ) = a \sin( \beta ) \\ b( \sin( \alpha ) \cos( \beta ) - \cos( \alpha ) \sin( \beta ) ) = a \sin( \beta ) \\ b( \sin( \alpha ) \ctg( \beta ) - \cos( \alpha ) ) = a \\ \ctg( \beta ) = \frac{ \frac{a}{b} + \cos( \alpha ) }{ \sin( \alpha ) } \\ \beta = \arcctg( \frac{ \frac{a}{b} + \cos( \alpha ) }{ \sin( \alpha ) } )$

отсюда находим AM:

$am = \frac{b}{ \sin( \arcctg( \frac{ \frac{a}{b} + \cos( \alpha ) }{ \sin( \alpha ) } ) ) }$