3−x < 3^x. Какое решение подходит к данной функции?
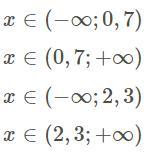
Ответы
Ответ:
четвертое х€(2,3;∞)
Объяснение
Дано неравенство.Линейная функция (3-х) убывающая, а показательная (3^х) возрастающая для всех х€R.
При х=0 3>1-неравенство не выполняется, значит возможные решения лежат в интервалах 2 и 4.
При х=0.7 2.3>2.158 -неравенство не выполняется, значит х=0.7 и бесконечно близкие к нему значения не входят в область решений. Возьмем х=0.74, получим 2.26>2.255 -опять не выполняется, а при х=0.742 2.258<2.260 -выполняется. Значит нижней границей интервала значение х=0.7 не является, поскольку при значениях 0.7<х<0.74 (например) неравенство не выполняется.
На 4м интервале неравенство верное для всех х этого интервала, включая даже х=2.3
Ответ: При х=1 значение 3-1-3^1=2-3=-1 (удовлетворяет). При х=0,7 значение левой части 3-0,7=0,3, правой части 3^0,7=2,158, не удовлетворяет, то есть решение между 0,7 и 1. Тогда диапазоны первый, во второй и третий не подходят. Ответом будет четвёртый диапазон. Функция 3-х-3^х уменьшающая с увеличением х, так как её производная равна -1-ln(3)*3^x уменьшается (3^x возрастает).
Ответ: 4 диапазон (от 2,3 до +бесконечности).
Объяснение: