Предмет: Алгебра,
автор: elena5001
решить логарифмическое выражение
Приложения:
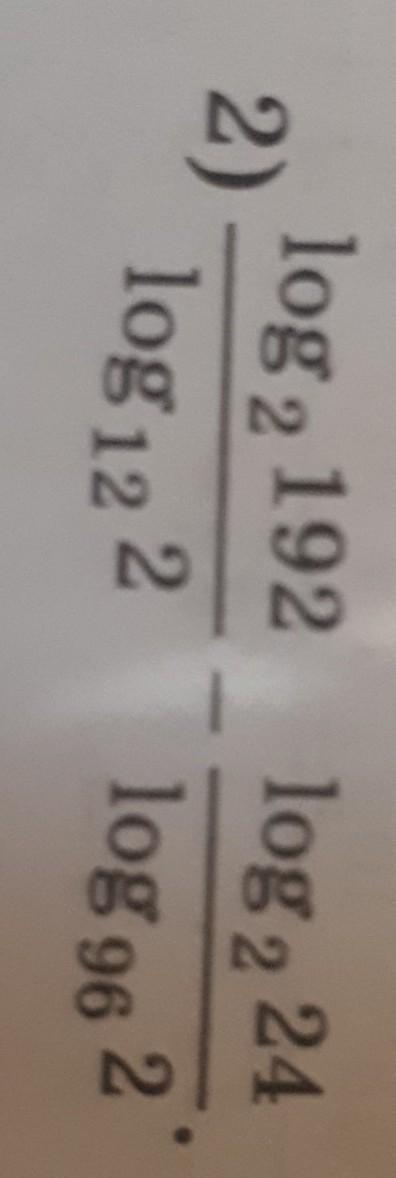
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: FaschenkoAndrey
Предмет: Физика,
автор: Gggggggghkdkdks
Предмет: Алгебра,
автор: usiknikoletta
Предмет: Биология,
автор: ксения7978
Предмет: Обществознание,
автор: НикаКоролёва