Предмет: Алгебра,
автор: serhee2
Помогите решить неравенство!!!
Приложения:
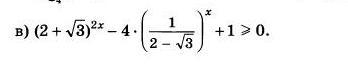
Ответы
Автор ответа:
0
Ответ:
x ∈ (-oo; -1] U [1; +oo)
Объяснение:
Начнем с того, что
Теперь делаем замену > 0 при любом х.
y^2 - 4y + 1 >= 0
D = (-4)^2 - 4*1*1 = 16 - 4 = 12 = (2√3)^2
y1 = (4 - 2√3)/2 = 2 - √3
(2 + √3)^x = 2 - √3 = 1/(2 + √3)
x1 = -1
y2 = (4 + 2√3)/2 = 2 + √3
(2 + √3)^x = 2 + √3
x2 = 1
x ∈ (-oo; -1] U [1; +oo)
Похожие вопросы
Предмет: Українська мова,
автор: mariahriplivaa
Предмет: Литература,
автор: vovan19871
Предмет: Математика,
автор: augulkasimova076
Предмет: История,
автор: ksushkay12
Предмет: Литература,
автор: svekla1006