ОЧЕНЬ СРОЧНО ДАМ КУЧУ БАЛЛОВ ПРОШУ ПОМОГИТЕ МНЕ МОЖНО ТОЛЬКО ОТВЕТ . ПОЖАЛУЙСТА
На плоскости даны окружности радиусов 4 и 11, расстояние между центрами которых равно 25. Длины их общих касательных равны:
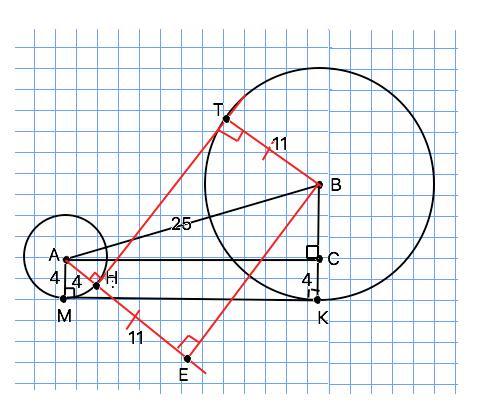
внешних внутренних
Ответы
Ответ: внешняя касательная=24, внутренняя - 20.
Объяснение: Пусть центры данных окружностей А и В,
АВ=25 - расстояние между центрами (дано);
внешняя касательная МК, внутренняя ТН.
АМ=4 - радиус меньшей окружности (дано) и перпендикулярен МК (свойство радиуса и касательной),
ВК=11 - радиус большей окружности перпендикулярен КМ.
а) внешняя касательная МК: Проведем АС параллельно МК. Четырехугольник АМКС - прямоугольник, СК=АМ=4 ⇒
ВС=ВК-СК=11-4=7
Треугольник АВС - прямоугольный.
По т. Пифагора АС=√(AB²-BC²)=√(25²-7²)=24
МК=АС=24 (ед. длины)
б)внутренняя касательная НТ:
Проведем радиусы АН и ВТ в точки касания. Из центра большей окружности проведем прямую параллельно ТН, продлим АН до пересечения с прямой из В в точке Е. Четырехугольник НТВЕ - прямоугольник (радиусы перпендикулярны касательной, противоположные стороны попарно параллельны и равны). АЕ=АН+НЕ=4+11=15; АВ=25 ( дано). По т.Пифагора из прямоугольного треугольника АВЕ катет ВЕ=√(AB²-AE²)=√(25²-15²)=20.
ТН=ВЕ=20 (ед. длины)