Предмет: Алгебра,
автор: dubrovinalenaЛена
Решите уравнение
√2sin(2x+pi/4)–√3sinx=sin2x+1
Ответы
Автор ответа:
0
/////////////////////////////////////////////
Приложения:
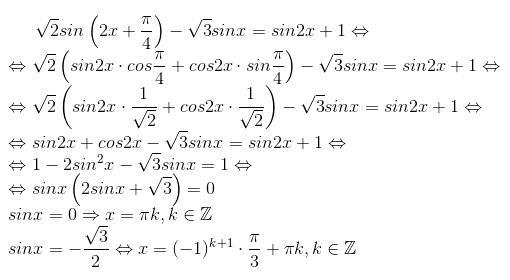
dubrovinalenaЛена:
cos pi/4 = корню из 2/2
Автор ответа:
1
сейчас напишу
написала внутри ответа, перезагрузи страницу...
кому как удобно...если нет специальных указаний...
считать удобнее от 0
Похожие вопросы
Предмет: Алгебра,
автор: lianakuznetsova325
Предмет: Алгебра,
автор: DOLWOE
Предмет: Другие предметы,
автор: viii7777
Предмет: Математика,
автор: lollipoop171
Предмет: Математика,
автор: Fiydydkdkkhdiydkdsid