Предмет: Математика,
автор: kirillromula
помогите пожалуйста решить
Приложения:
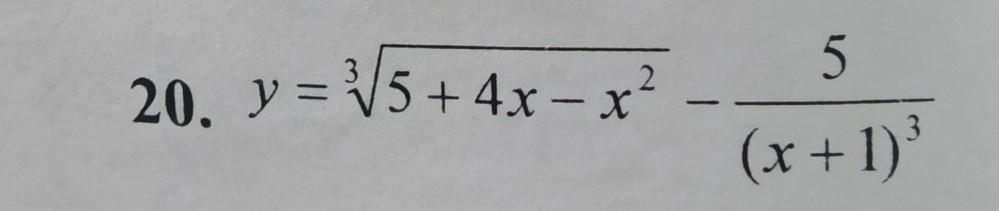
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: saidovbobur658
Предмет: Английский язык,
автор: polyaalcheeva
Предмет: Математика,
автор: jekreowtieor
Предмет: Алгебра,
автор: марина1358
Предмет: Математика,
автор: Абдулла21