Question

Помогите , пожалуйста .Привести уравнение кривой второго порядка к каноническому виду . Определить ее тип, выписать параметры и построить .

Answer 1

Дано уравнение x² - 4y² + 4x - 8y - 2 = 0.

Выделим полные квадраты.

(x² + 4x + 4) - 4 - (4y² + 8y +4) + 4 - 2 = 0.

Получаем (x + 2)² - 4 - 4(y² + 2y +1) + 4 - 2 = 0.

(x + 2)²  - 4(y² + 2y +1)  = 2.   Разделим обе части уравнения на 2.

((x + 2)²/2)  - (4(y + 1)²)/2)  = 1. Это уравнение гиперболы, приведём его к каноническому виду.

((x + 2)²/(√2)²)  - ((y + 1)²)/(√2/2)²)  = 1.

Отсюда получаем основные параметры гиперболы.

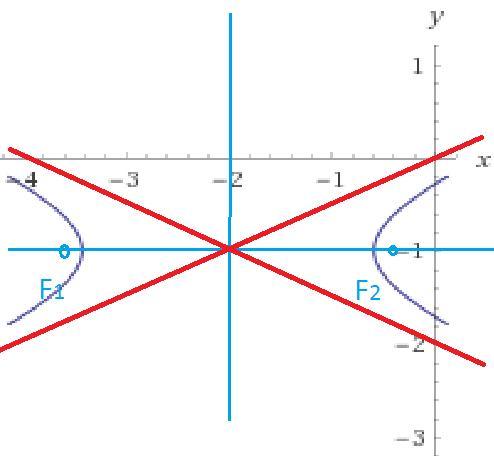
Центр (-2; -1), полуоси a = √2, b = 1/√2 = √2/2.

Детальнее и график - во вложениях.