Предмет: Алгебра,
автор: lida5869
помогите пожалуйста задание: "ж" и "з"
Приложения:
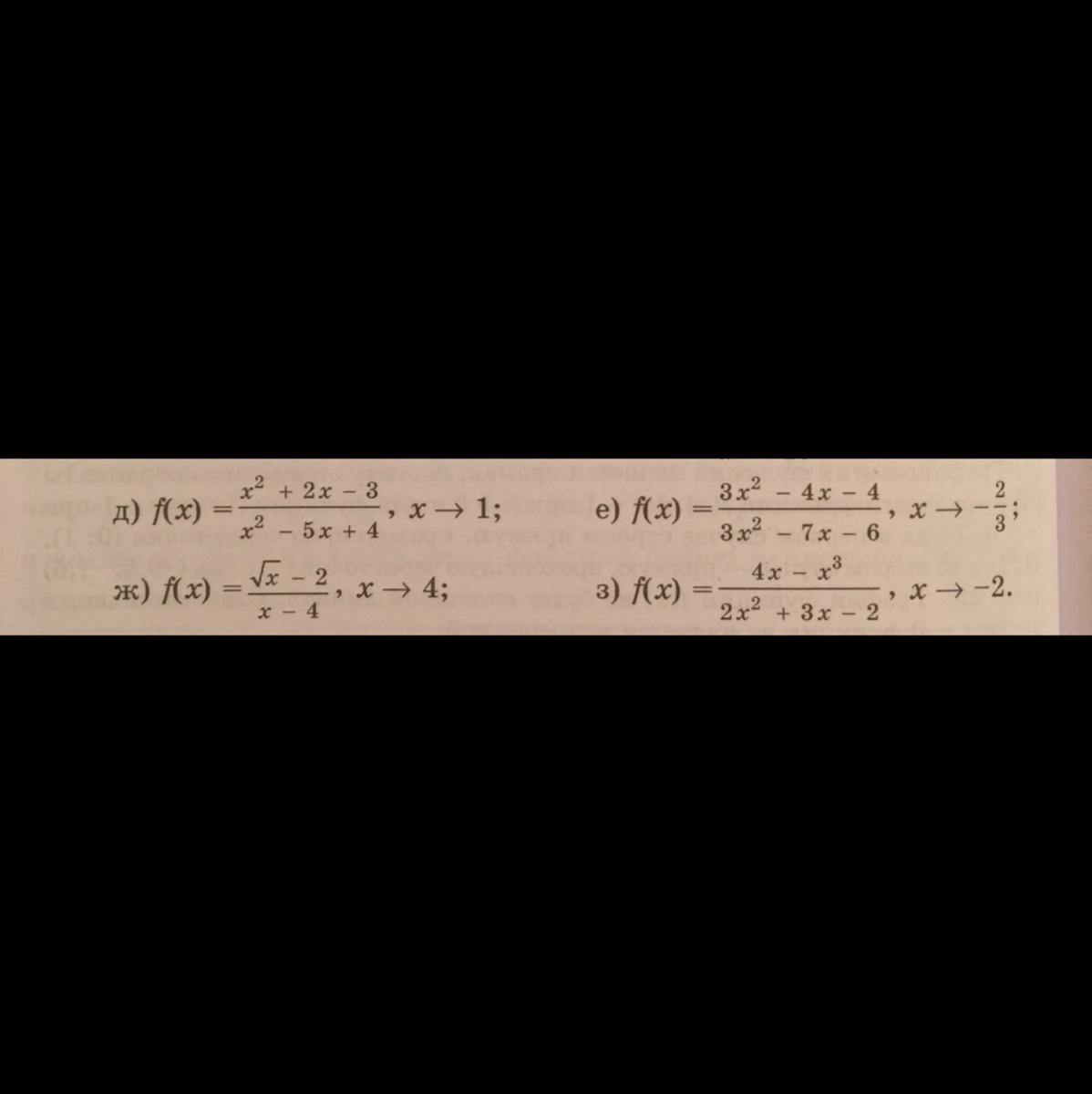
Ответы
Автор ответа:
1
Пояснение:
lida5869:
спасибо большое ❤️
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: olenatkachuk16
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Liatlant
Предмет: Математика,
автор: aminohka