Предмет: Алгебра,
автор: anteagrin3333
Решите пожалуйста срочно!!!!!
Приложения:
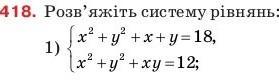
Ответы
Автор ответа:
1
anteagrin3333:
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: laninaa932
Предмет: Алгебра,
автор: jalubluvm
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: хиялмодица