Question

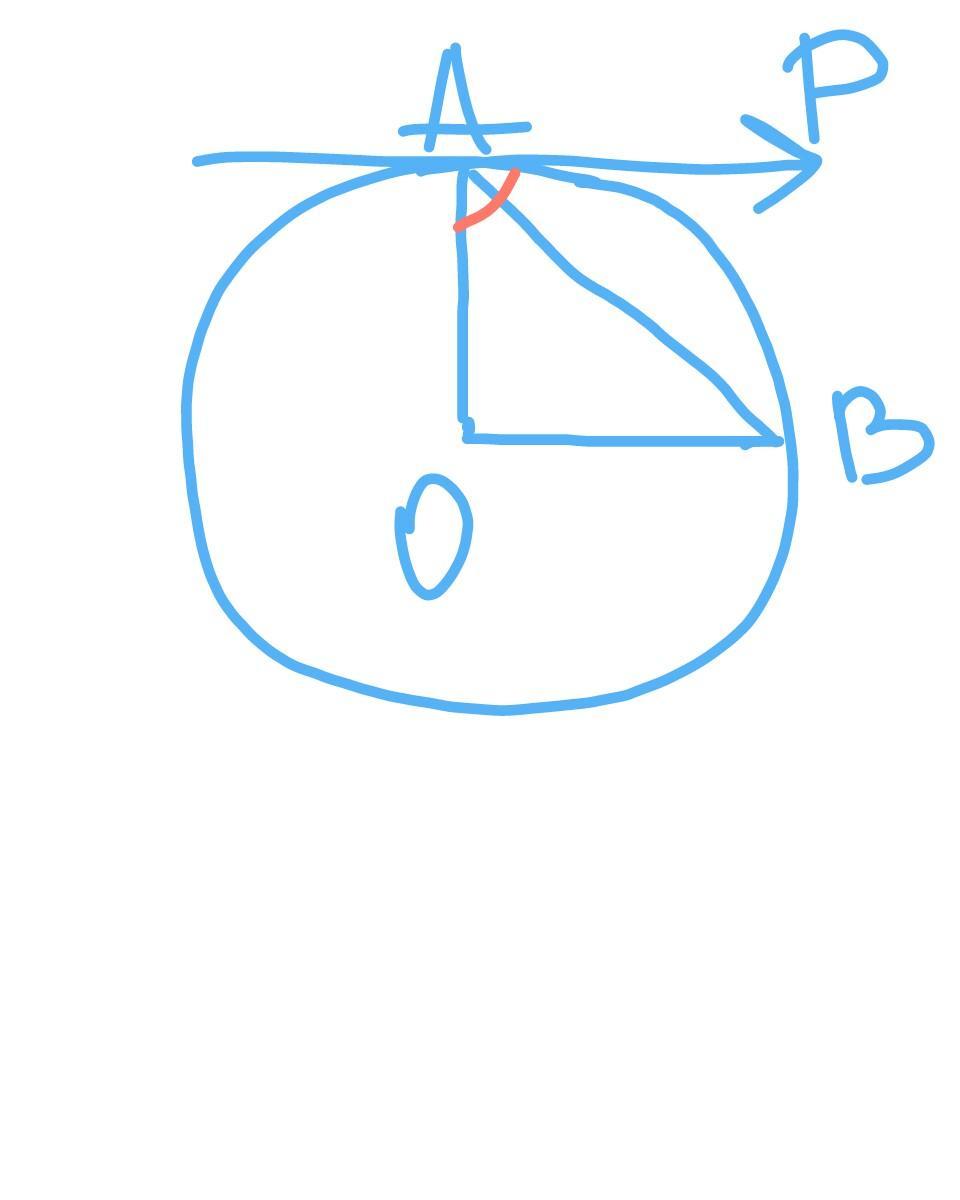
на рисунке АР касательная, угол PAB 45°, 0 центр окружности, АВ 4 см, найдите ОА​

Answer 1

Ответ:

2$\sqrt{2}$

Пошаговое объяснение:

Треугольник АОВ равнобедренный т.к. два его катета это два одинаковых радиуса окружности. Соответственно самое простое можем найти через теорему Пифагора не задействовав углы и прочее. АВ - гипотенуза этого треугольника. АОВ прямоугольный т.к. углы при основании равны (45 градусов). Значит AB^2 = OB^2 + AO^2. Т.к. ОВ и АО равны, значит АВ^2 = 2ОА^2. Далее 16 = 2x^2. x^2 = 8. x = $\sqrt{8}$ = 2$\sqrt{2}$