Предмет: Математика,
автор: nsemenova26
можете подробно объянсить как считать?
Приложения:
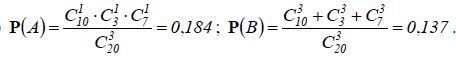
Ответы
Автор ответа:
1
Ответ:
Формула количества сочетаний
Отсюда
и
Тогда
Результат деления приблизительное!
Результат деления приблизительное!
Аноним:
\approx - знак приближения.
Похожие вопросы
Предмет: Українська мова,
автор: shmona7282
Предмет: Математика,
автор: Mafa3464
Предмет: Алгебра,
автор: yapridumalshutku
Предмет: Математика,
автор: ibr3
Предмет: Литература,
автор: makskoz02