Предмет: Математика,
автор: tyiara66
Вычислить пределы, используя зачемательные пределы или эквивалентные бесконечные малые функции
Приложения:
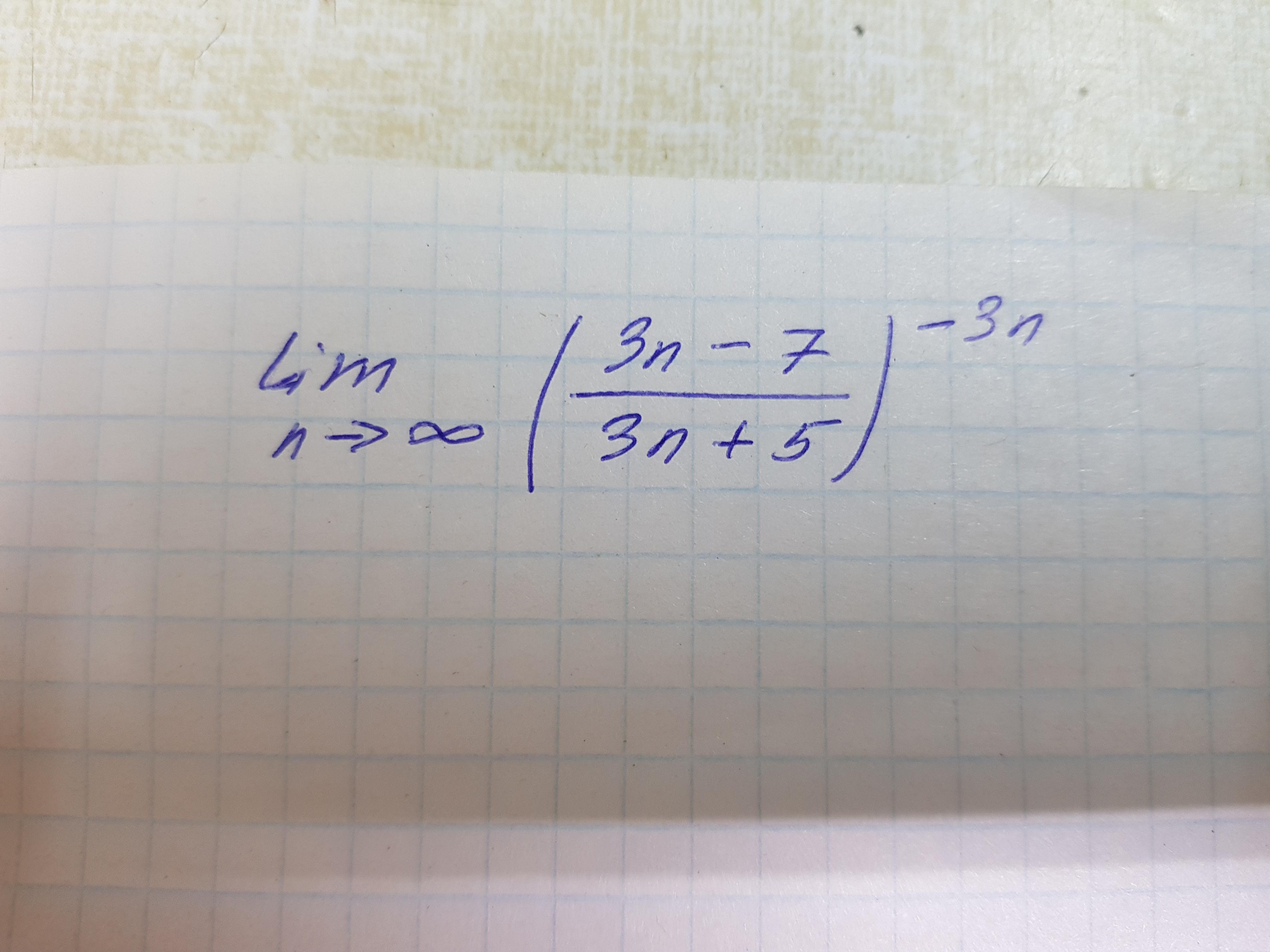
Ответы
Автор ответа:
1
По второму замечательному пределу:
Похожие вопросы
Предмет: Английский язык,
автор: makarpereverzev1564
Предмет: Беларуская мова,
автор: tomamerikano173
Предмет: Математика,
автор: bykolcunanastasia
Предмет: Математика,
автор: папа274
Предмет: Литература,
автор: 123451291