Предмет: Математика,
автор: Sunshine1408
Помогите, пожалуйста
Найти значение производной
Приложения:
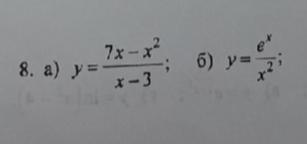
Ответы
Автор ответа:
1
Пошаговое объяснение:
Можно записать след.образом
Похожие вопросы
Предмет: Математика,
автор: s83000
Предмет: Математика,
автор: s83000
Предмет: Математика,
автор: s83000
Предмет: Химия,
автор: Аноним