Предмет: Математика,
автор: gdhdhdghdb
Помогите с уравнениямиии прошуу помогите пожалуйста! дам 50 баллов
Приложения:
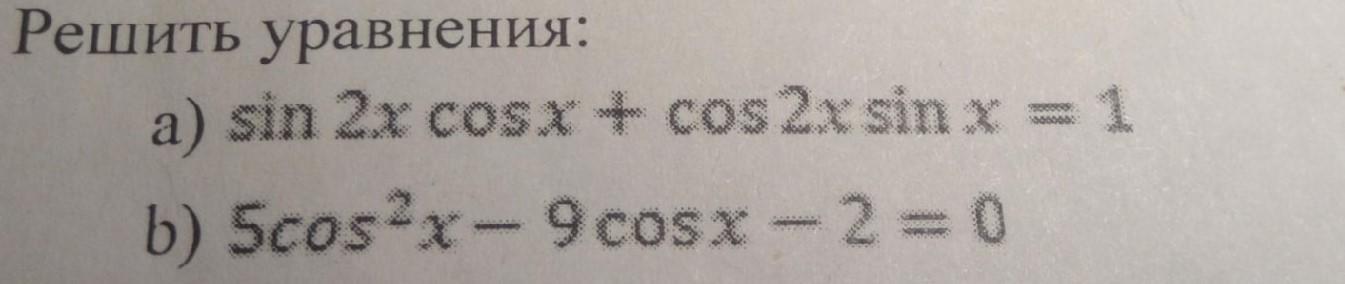
Ответы
Автор ответа:
2
matilda17562:
Ошибка в первом уравнении?
исправила, спасибо
Автор ответа:
1
Ответ:
а) π/6 + 2πn/3, где n∈ Z.
б) ± (π - аrccos1/5) + 2πn, где n∈ Z..
Пошаговое объяснение:
а). sin2x•cosx + cos2x•sinx = 1
sin(2x + x) = 1
sin3x = 1
3x = π/2 + 2πn, где n∈ Z
x = π/6 + 2πn/3, где n∈ Z
Ответ: π/6 + 2πn/3, где n∈ Z.
b). 5cos²x - 9cosx - 2 = 0
Пусть сosx = t, ltl ≤ 1, тогда
5t² - 9t - 2 = 0
D = 81 + 40 = 121
t1 = (9+11)/10 = 2, не удовлетворяет условию замены
t2 = (9-11)/10 = -1/5.
Получили, что
сosx = - 1/5
х = ± аrccos(-1/5) + 2πn, где n∈ Z
х = ± (π - аrccos1/5) + 2πn, где n∈ Z.
Ответ: ± (π - аrccos1/5) + 2πn, где n∈ Z..
Похожие вопросы
Предмет: Химия,
автор: brigalow
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: makdg02
Предмет: Математика,
автор: Дарья151210
Предмет: Математика,
автор: 2461323а