Предмет: Геометрия,
автор: denzpua20
Помогите решить задачу: Окружность с центром I, вписанная в треугольник АВС, касается сторон АВ и ВС в точках С0 и А0 соответственно. Окружность, проходящая через точки В и I, пересекает стороны АВ и ВС в точках X и Y. Докажите, что середина отрезка XY лежит на прямой А0С0.
РИСУНОК:
Приложения:
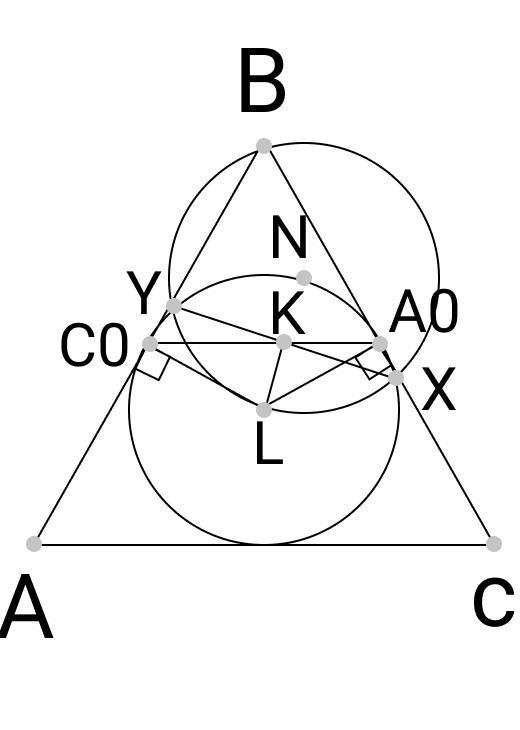
Simba2017:
рисунок неверный хотя бы потому, что треугольник не равносторонний по условию
Ответы
Автор ответа:
1
Из точки описанной окружности на прямые сторон треугольника опущены перпендикуляры. Основания перпендикуляров лежат на прямой Симсона.
Точка I лежит на биссектрисе угла B, следовательно делит дугу XY пополам. Пусть Bo - середина хорды XY. Тогда IBo - серединный перпендикуляр к XY (хорды IX и IY равны, стягивают равные дуги).
I - точка на окружности, описанной около треугольника XBY. IAo, IBo, ICo - перпендикуляры, опущенные на стороны треугольника XBY. Основания перпендикуляров Ao, Bo, Co лежат на прямой Симсона.
Приложения:
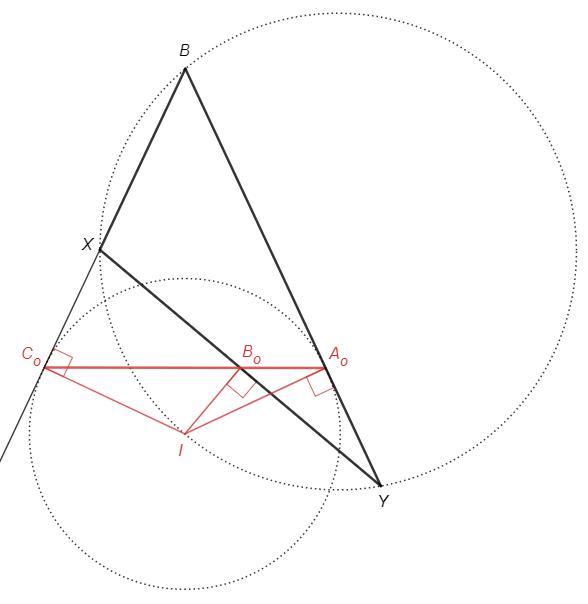
интересное доказательство, но школьникам наверное не понять. Спасибо!
Похожие вопросы
Предмет: Английский язык,
автор: student19228
Предмет: Английский язык,
автор: Jdhfjdjc
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: juljabezdolnya