Предмет: Математика,
автор: asim02022003
ДАЮ МНОГО БАЛЛОВ ЗА РЕШЕНИЕ
Приложения:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Прости, может быть не правильно... мы так в колледже решаем
Приложения:
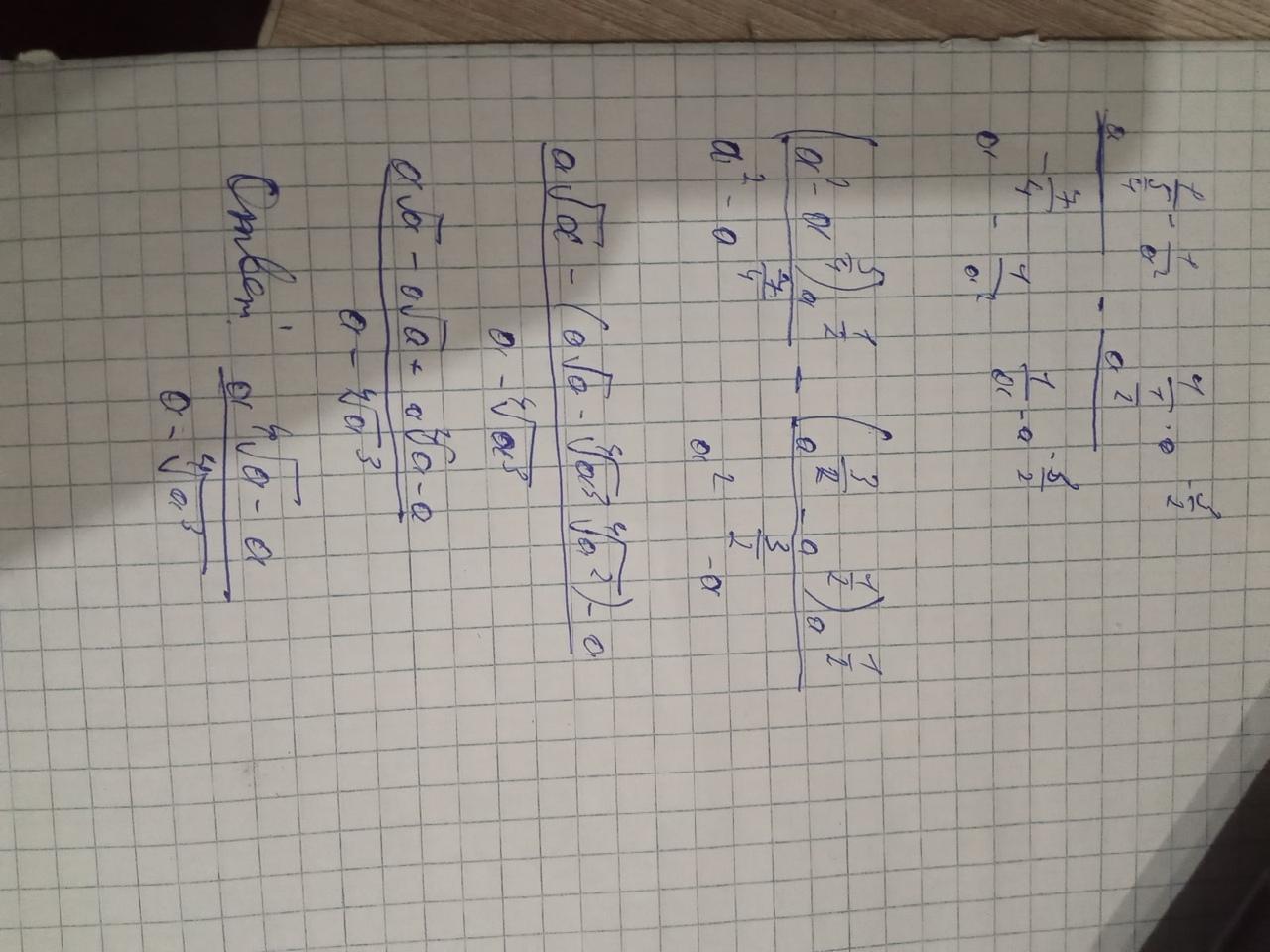
asim02022003:
А 1 не знаешь?
Извини, первый не могу вспомнить чет(
Все равно спасибо))
Автор ответа:
0
Ответ:
1)
2)
Похожие вопросы
Предмет: Математика,
автор: oleghigolica123
Предмет: Физика,
автор: KonladCPS
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: sakyra8