Предмет: Алгебра,
автор: mvogul2004
Очень срочно! Очень подробное решение и график, пожалуйста
Приложения:
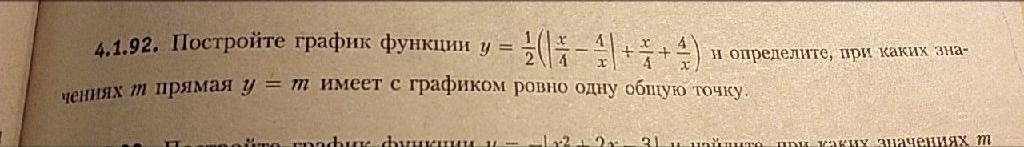
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Объяснение:
Раскроем модуль:
Тогда:
1)
2)
Построим график по точкам (см. фото 1)
При m=-1, m=1 прямая y=m имеет с графиком ровно 1 общую точку. (см. фото 2)
Приложения:


Похожие вопросы
Предмет: Английский язык,
автор: marina474859
Предмет: Математика,
автор: saschabctkachenko
Предмет: Геометрия,
автор: veronikasnajder17
Предмет: Литература,
автор: ledisaif
Предмет: Математика,
автор: AnnaMiloshenkoand66