Предмет: Математика,
автор: Alexcey47
вычислить интегралл
Приложения:
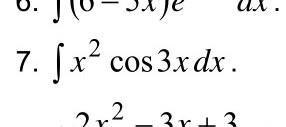
Ответы
Автор ответа:
1
Ответ на листках решено
Приложения:



Suleiman45:
Надеюсь правильно
Автор ответа:
1
Похожие вопросы
Предмет: Химия,
автор: nadakarpuk00
Предмет: Математика,
автор: ayanallahverdiyeva79
Предмет: Английский язык,
автор: annwnnwkeskks
Предмет: Математика,
автор: Оалвб
Предмет: Алгебра,
автор: Екатерина1457536