Предмет: Алгебра,
автор: Аноним
|x|⋅(5x+1)^6−4096*|x|/(1/(x −1/8))−(4/|3,5−2x|) ≥ 0
Решите неравенство методом интервалов, заменяя множители в числителе и знаменателе более простыми множителями того же знака
Приложения:

Ответы
Автор ответа:
4
Сначала преобразовали знаменатель,потом избавились от трёхэтажной дроби. Нашли ОДЗ. После чего разложили на множители числитель
Уравнение
Имеет два действительных корня ,следовательно оно равносильно разложению (x+1)(x-3/5)
Дальше метод интервалов ,видим в числители произведение из двух множителей ,коэффициенты перед х все положительные ,следовательно чередование начнётся с плюса,а дальше наносим наши ограничения и корни
Так как неравенство нестрогое ,что можно делить на то ,что всегда положительное ,в нашем случаи - модули ,но нули этих выражений - наши корни
Приложения:
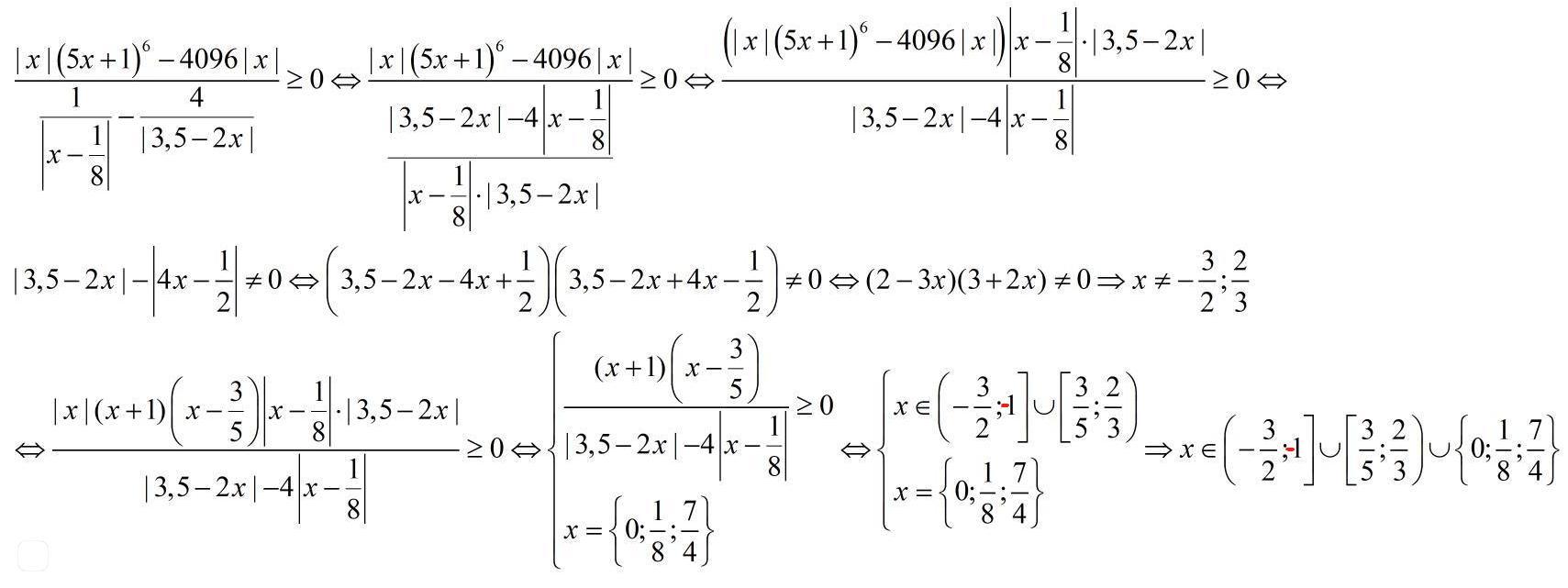
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: asemgul293
Предмет: Геометрия,
автор: pborysiuk
Предмет: Математика,
автор: кристина1542