Question

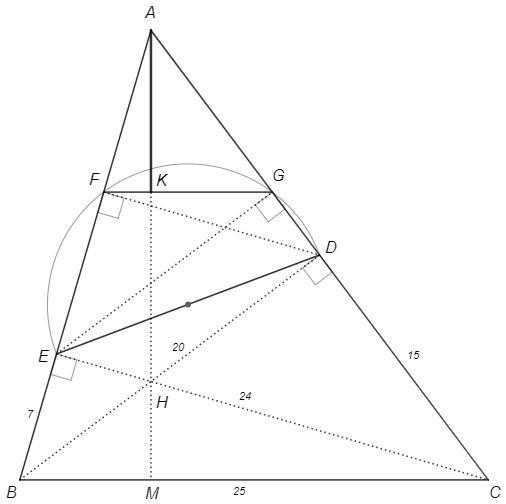
H - ортоцентр остроугольного треугольника ABC, точки D и E - основания высот, проведенных соответственно из вершин B и C. Окружность с диаметром DE пересекает стороны AB и AC еще раз соответственно в точках F и G. Отрезки FG и AH пересекаются в точке K. Если BC=25, BD=20 и BE=7, то найдите длину отрезка AK.

Answer 1

Отрезок, соединяющий основания высот, отсекает подобный треугольник.

DAE~BAC

Коэффициент подобия AD/AB =cosA  

F, G - основания высот в DAE (DFE, DGE опираются на диаметр DE)

FAG~DAE

Таким образом FAG~BAC, k=cosA^2

FG||BC (F=B) => AK - высота в FAG  

cosA = -cos(B+C) = sinBsinC -cosBcosC =

24/25 *20/25 - 7/25 *15/25 =3/5  

Но косинус угла С тоже равен 3/5, следовательно A=C.

Равнобедренный треугольник, высоты к боковым сторонам равны.

AM=CE =24

AK =cosA^2 *AM = 24*9/25 =8,64