Предмет: Математика,
автор: LLocika
Решите, пожалуйста, 2 примера (вариации). Ответ должен получиться: e) 3; f) 1; 2; 3; 4.
Приложения:
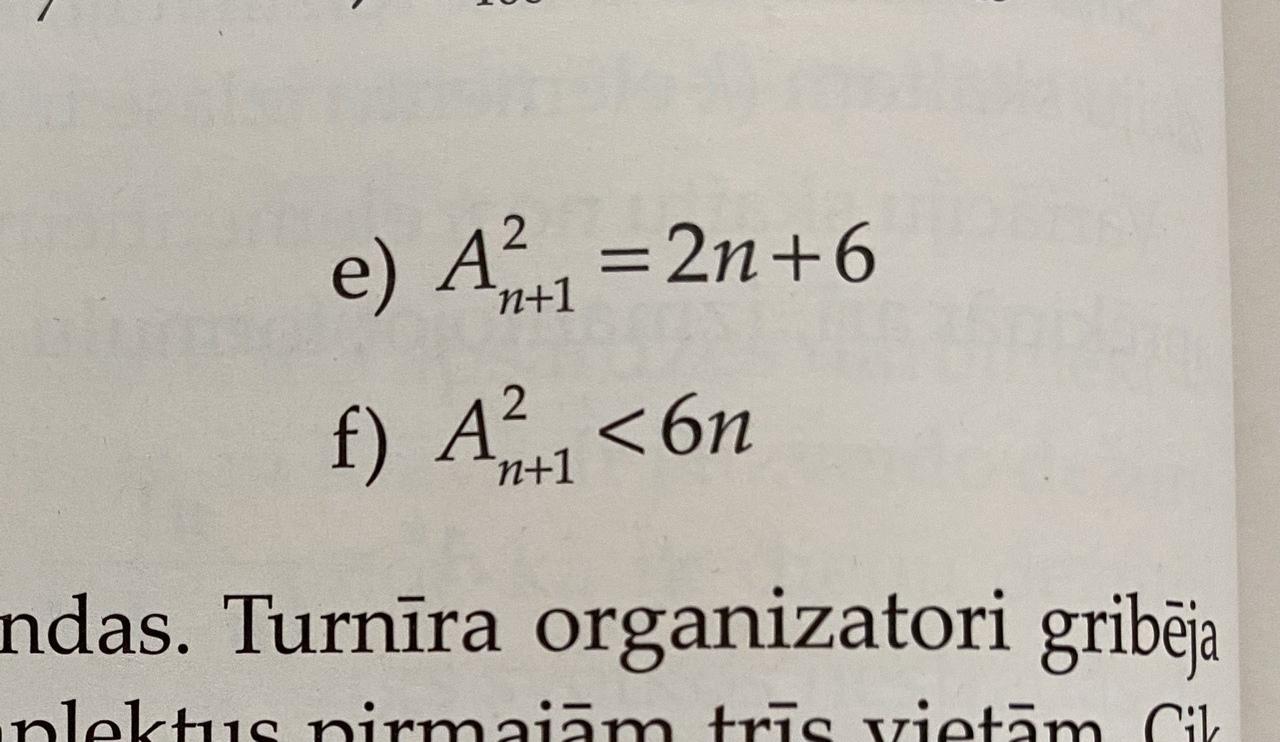
Ответы
Автор ответа:
1
e)
Ответ: 3
================
f)
Ответ: 1; 2; 3; 4
LLocika:
Спасибо огромное!
Похожие вопросы
Предмет: Физика,
автор: seeie
Предмет: Химия,
автор: Popovichinna1970110
Предмет: Математика,
автор: annakordina2009
Предмет: Химия,
автор: gulbisru
Предмет: Математика,
автор: Vova15112006