Допоможіть БУДЬ ЛАСКА!!!
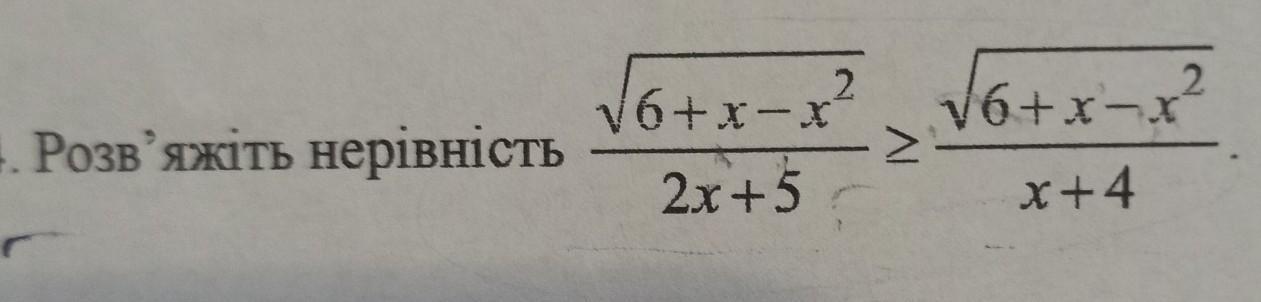
Ответы
Ответ:
Пошаговое объяснение:

Ответ:
x∈[-2; -1] ∪ {3}
Пошаговое объяснение:
Определим область допустимых значений неравенства
:
2x+5≠0, x+4≠0, 6+x-x²≥0 или
x≠ -2,5, x≠ -4. Решаем сначала уравнение 6+x-x²=0 или x²-x-6=0:
D= (-1)²-4·1·(-6)=1+24=25=5²
x₁=(1-5)/2= -2, x₂=(1+5)/2= 3.
Тогда методом интервалов определим знак выражения
6+x-x²= -(x+2)(x-3):
-- · -- · -- = -- 0 -- · + · -- = + 0 -- · + · + = --
-∞ -------[-100]-----------[-2]-----------[0]-----------------[3]---------[100]---------->+∞
Значит, ОДЗ: [-2; 3].
Здесь можно разделить выражение левой части. Так как в ОДЗ , то для этого неравенства достаточно рассмотреть оставшийся часть:
В силу ОДЗ, достаточно решить неравенство
(x+1)·(2·x+5)·(x+4)≤0
Методом интервалов определим знак выражения (x+1)·(2·x+5)·(x+4):
-- · + · + = -- 0 + · + · + = +
-∞ ------(-4)-----(-2,5)------[-2]----[-1,5]-------[-1]------[0]---------[3]----------->+∞
Отсюда x∈[-2; -1].
Напишем ответ, учитывая нули выражения 6+x-x²:
x∈[-2; -1] ∪ {3}.