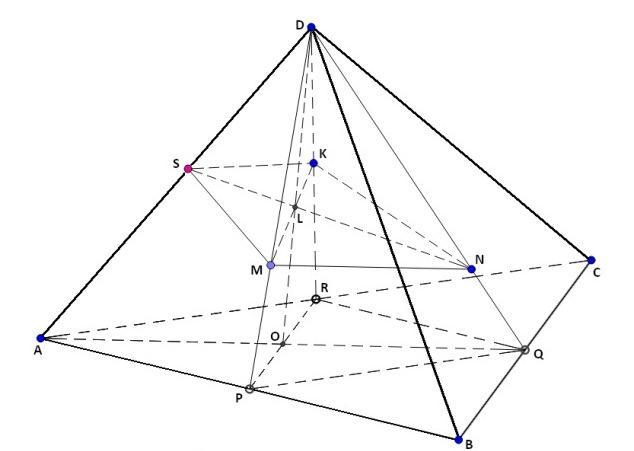
В піраміді ABCD на медіанах DP, DQ, DR граней ABD, BCD, CAD відповідно задано точки M, N, K, для яких DM : MP = 2:1, DN : NQ = 3:1, DK:KR =1:1, S - точка перетину прямої AD площиною MNK . Знайти відношення
DS: SA.
Ответы
Відповідь:
DS:SA=6:7.
Пояснення:
Виконаємо рисунок, для побудови перетину використаємо метод
внутрішнього проектування: (AQ)∩(PR)=O, (DO)∩(MK)=L, (NL)∩(AD)=S, де S – шукана точка перетину прямої (AD) площиною (MNK).
Зауважимо, що чотирикутник ARQP – паралелограм, а тому точка О є серединою обох його діагоналей. Розглянемо трикутник DPR: точки О і K є серединами своїх сторін, а тому PD||KO і PD=2·KO; з умови маємо, що MD=⅔·PD, а тому MD:KO=4:3. З подібності трикутників MDL i KOL маємо DL:OL=MD:KO, а тому DL:OL=4:3.
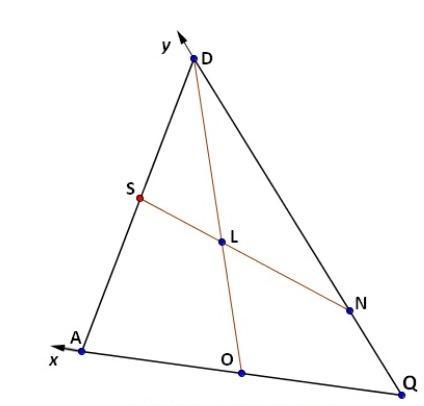
Розглянемо трикутник QAD, введемо афінну систему координат. Нехай точка Q(0;0) – початок координат, напрям вісі абсцис – від точки Q до точки А, нехай A(2;0), напрям вісі ординат – від Q до D, нехай D(0;4).
Тоді, з урахуванням умови, координати О(1;0), N(0;1).
Обчислимо координати точки L(x; y):
вектори DO(1;-4); DL(х; y- 4), причому DL=4/7 DO, а тому L (4/7;12/7). Вектор NL(4/7;5/7)||(4;5), а тому рівняння прямої NL x=4t; y=1+5t, tєR
Рівняння прямої (АD) за двома точками : (х-0)/(2-0)=(у-4)/(0-4) або
2x + y- 4= 0.
Знайдемо координати точки S =(NL)∩(AD), розв’язавши систему рівнянь:
2x + y- 4= 0;
x=4t; ⇒2*4t+1+5t-4=0 ⇒8t+5t=3 ⇒ 13t=3 ⇒ t=3/13;
y=1+5t.
x=4*3/13=12/13;
y=1+5*3/13=1+15/13=28/13.
Тобто S(12/13;28/13).
А тоді вектори DS(12/13;-24/13)=12/13*(1;-2); SA(14/13;-28/13)=14/13*(1;-2).
і шукане відношення DS:SA=6:7.
Відповідь: DS:SA=6:7.