Хоть что-то из этого...
Даны координаты вершин пирамиды A1 А2 А3 А4. Найти:
а) угол между рёбрами А1 А2 и А1 А3;
б) площадь грани А1 А2 А3;
в) уравнение плоскости А1 А2 А3;
г) уравнение высоты, проходящей через А4;
д) объём пирамиды.
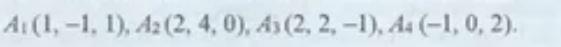
Ответы
Для удобства примем координаты вершин пирамиды АВСD :
A(1, -1, 1), B(2, 4, 0) , C(2, 2, -1), D(-1, 0, 2).
а) угол между рёбрами А1 А2 и А1 А3 (АВ и АС).
Вектор АВ = (2-1=1; 4-(-1)=5; 0-1=-1) = (1; 5; -1). Модуль равен √27.
Вектор АС = (1; 3; -2). Модуль равен √14.
Находим их скалярное произведение:
АВ * АС = 1 + 15 + 2 = 18.
cos(АВ * АС) = 18/(√27*√14) ≈ 0,9258.
Угол равен arc cos 0,9258 = 0,3876 радиан или 22,2077 градуса.
б) площадь грани А1 А2 А3 (АВС).
Векторы АВ и АС получены, находим их векторное произведение.
Вектор АВ = (1; 5; -1), вектор АС = (1; 3; -2).
i j k | i j
1 5 -1 | 1 5
1 3 -2 | 1 3 = -10i - 1j + 3k + 2j +3i - 5k = -7i + 1j - 2k.
Нормальный вектор к плоскости АВС равен (-7; 1; -2).
Площадь АВС равна половине модуля векторного произведения:
S = (1/2)*√(49 + 1 + 4) = √54/2 ≈ 3,674.
в) уравнение плоскости А1 А2 А3 (АВС);
Составим его по заданным координатам точки А(1, -1, 1) и полученному нормальному вектору плоскости АВС(-7; 1; -2).
-7(x - 1) + 1(y + 1) - 2(z - 1) = -7x + 7 + y + 1 - 2z + 2 = -7x + y - 2z + 10.
г) уравнение высоты, проходящей через А4 (D).
Направляющий вектор высоты из точки D - это нормальный вектор плоскости АВС.
Уравнение прямой DO по координатам точки D и направляющему вектору ABC: (x + 1)/(-7) = y/1 = (z - 2)/(-2).
д) объём пирамиды. Для этого находим вектор AD = (-2; 1; 1).
Находим объём пирамиды как (1/6) модуля смешанного произведения векторов АВ и АС (-7; 1; -2) на AD(-2; 1; 1).
V = (1/6)*(14 + 1 - 2) = (13/6) ≈ 2,17 куб.ед.