Треба допомога, це треба доказати з допомогою одиничного кола
Буду вдячний.

Ответы
Ответ:
согласно формулам приведения cos(π/2+a)= -sin a, подставляем и получаем sina=sina, ч.т.д.
Відповідь:
Пояснення:
Правило "ослика":
1. Задаємо собі питання: «Чи змінюється назва функції на кофункцію?» (Тобто синнус на косинус, косинус на синус, тангенс на котангенс і котангенс на тангенс).
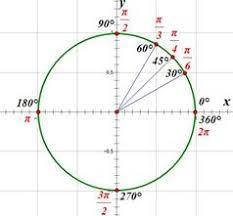
Щоб відповісти на це питання потрібно, махнути головою уздовж осі, на якій розташовується ключова точка (див. мал.)
Якщо мотаєте головою уздовж горизонтальної прямої, тому що ключова точка розташовується на ній, то ви, якби, відповідаєте «ні» на запитання «Чи змінюється назва функції на кофункцію?»
Якщо ви киваєте головою уздовж вертикальної прямої, тому що ключова точка розташовується на ній, то ви відповідаєте «так» на запитання «Чи змінюється назва функції на кофункцію?».
В даному випадку π/2 знаходиться на осі 0у, тому функція косинус міняється на синус, кут попадає в другу чверть, а косинус там від'ємний (див мал.2)