Предмет: Алгебра,
автор: Lev678
Помогите решить алгебру
Приложения:

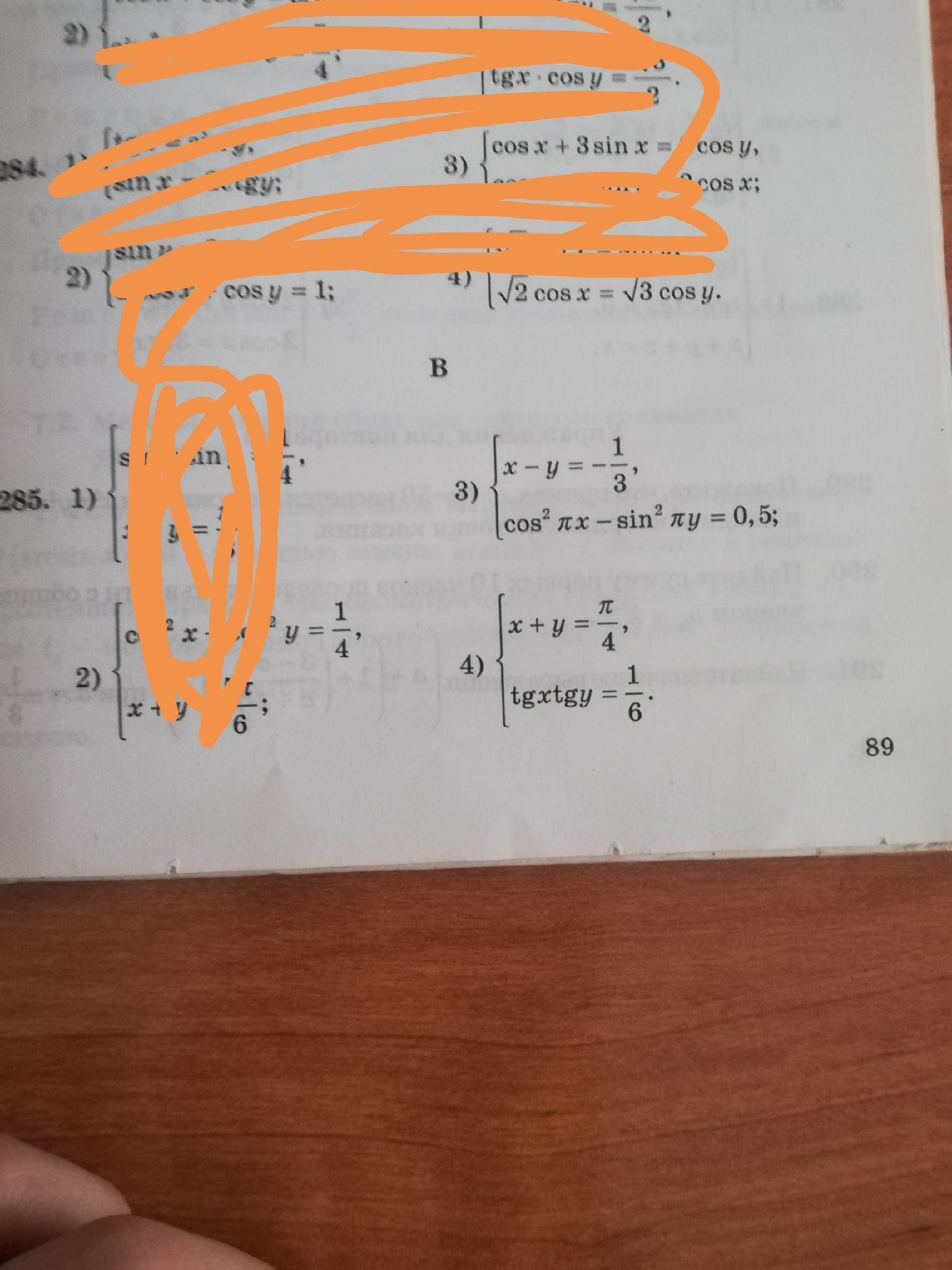
Ответы
Автор ответа:
1
282.3
285.4
Остальные варианты решаются аналогично.
saddatimov:
добавил решение второй задачи
Можете написать :) 100 балов всё таки. Если хотите я повторно создам +100 баллов будет еще.
UP https://znanija.com/task/33920439
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Английский язык,
автор: nabiyev003
Предмет: Геометрия,
автор: stive8490
Предмет: Биология,
автор: Борода11111
Предмет: Литература,
автор: brozher