Предмет: Алгебра,
автор: Улутов
вычислите интегралы
решите срочно пожалуйста
Приложения:
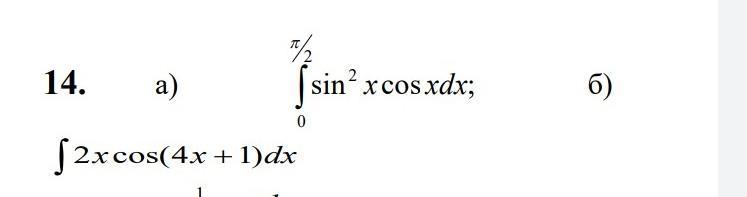
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: lenanaumenko69
Предмет: Английский язык,
автор: nastia54864
Предмет: Математика,
автор: noahtashaev
Предмет: Химия,
автор: andreyem2000
Предмет: Биология,
автор: rednik1