20 балов помогите....................
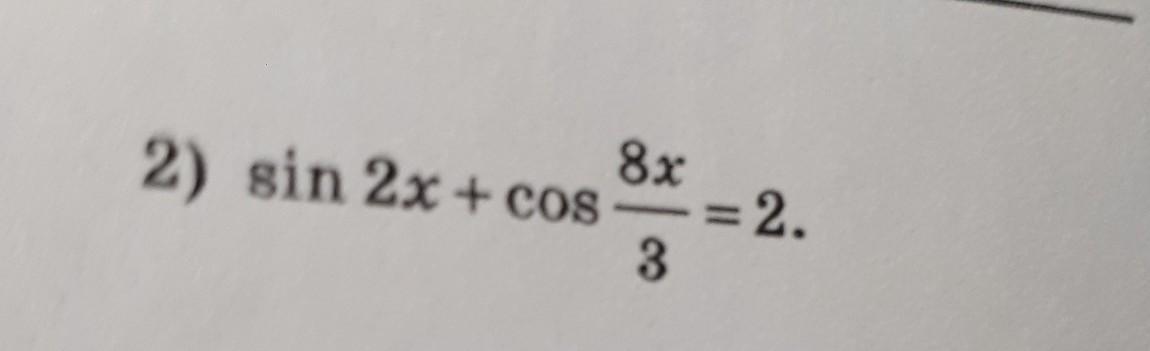
Ответы
Сумма может равняться только тогда двум, когда значения обеих функций одновременно равны по единице. Но если синус равен единице, то 2х=π/2 +2πn; n∈Z; х=π/4+πn;
А если косинус равен единице. то 8х/3=2πn; n∈Z; х=3πn/4; n∈Z;
А одновременно они достигают одного и того же значения равного единице, когда х= 9π/4 +3πn; n∈Z

Автор первого решения абсолютно правильно заметил, что поскольку синус и косинус не могут принимать значения, большие 1, их сумма равна 2 тогда и только тогда, когда каждый из них равен 1. Отсюда
Остается решить уравнение
Поскольку правая часть делится на 3, левая часть также должна делиться на 3, а поскольку 4 и 3 взаимно просты, n+1 делится на 3, то есть n+1=3m. Отсюда 12m=3(k+1); k+1=4m. Итак, n=3m-1; k=4m-1. Воспользовавшись любым из полученных равенств, находим x:
Ответ: