Предмет: Математика,
автор: ivansyrodeev
найти производную функции
Приложения:
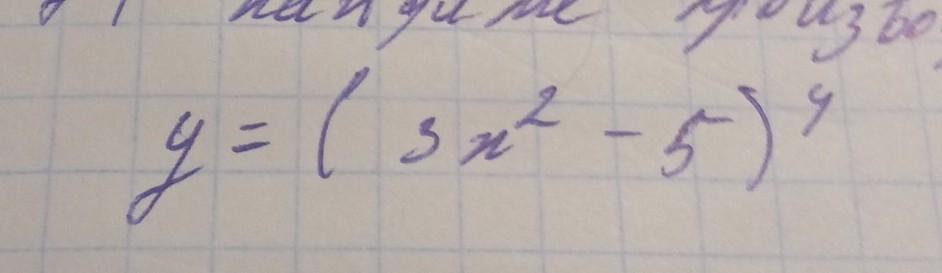
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y(x) = u(v),
где
Похожие вопросы
Предмет: Обществознание,
автор: ellis0440
Предмет: Физика,
автор: daundeadinside228
Предмет: Физика,
автор: daundeadinside228
Предмет: География,
автор: ДарьяВишневская