Предмет: Алгебра,
автор: MizoriesKun
Найти частное решение (подробный ответ )
Приложения:
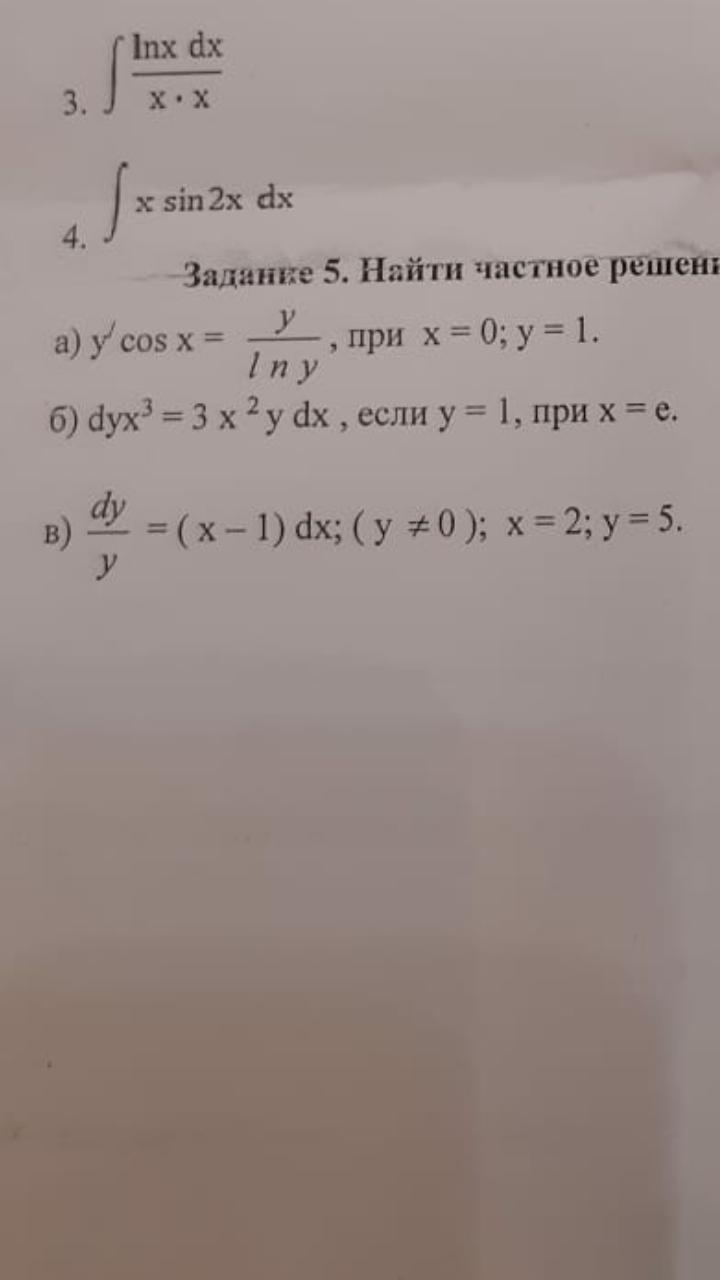
Ответы
Автор ответа:
21
MizoriesKun:
Высший пилотаж )) Спасибо .
Похожие вопросы
Предмет: Русский язык,
автор: Love19461976
Предмет: Геометрия,
автор: OtlicnikP
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Рудик010
Предмет: География,
автор: elena241083