Предмет: Математика,
автор: teacher22
ЛОГАРИФМЫ!!! ОЧЕНЬ СРОЧНО!!! ПОМОГИТЕ ПОЖАЛУЙСТА 5 НОМЕР
Приложения:
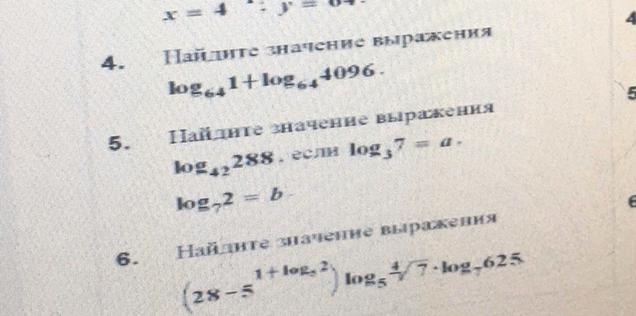
Ответы
Автор ответа:
1
Ответ:
Воспользуемся свойствами логарифмов:
logₐ1 =0, logₐa=1, logₐx*logₓa =1, logₐ(b*c) =logₐb+logₐc,
,
4. log₆₄1+log₆₄4096=0+log₆₄64²=2·log₆₄64=2·1=2
5.
6.
Автор ответа:
1
Ответ: во вложении Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Математика,
автор: maksim144l
Предмет: Математика,
автор: maksim144l
Предмет: Математика,
автор: maksim144l
Предмет: География,
автор: Настюша8881