Предмет: Алгебра,
автор: klimovrim2018
Помогите с пределами. Правилом Лопиталя нельзя. Даю много баллов.
Приложения:
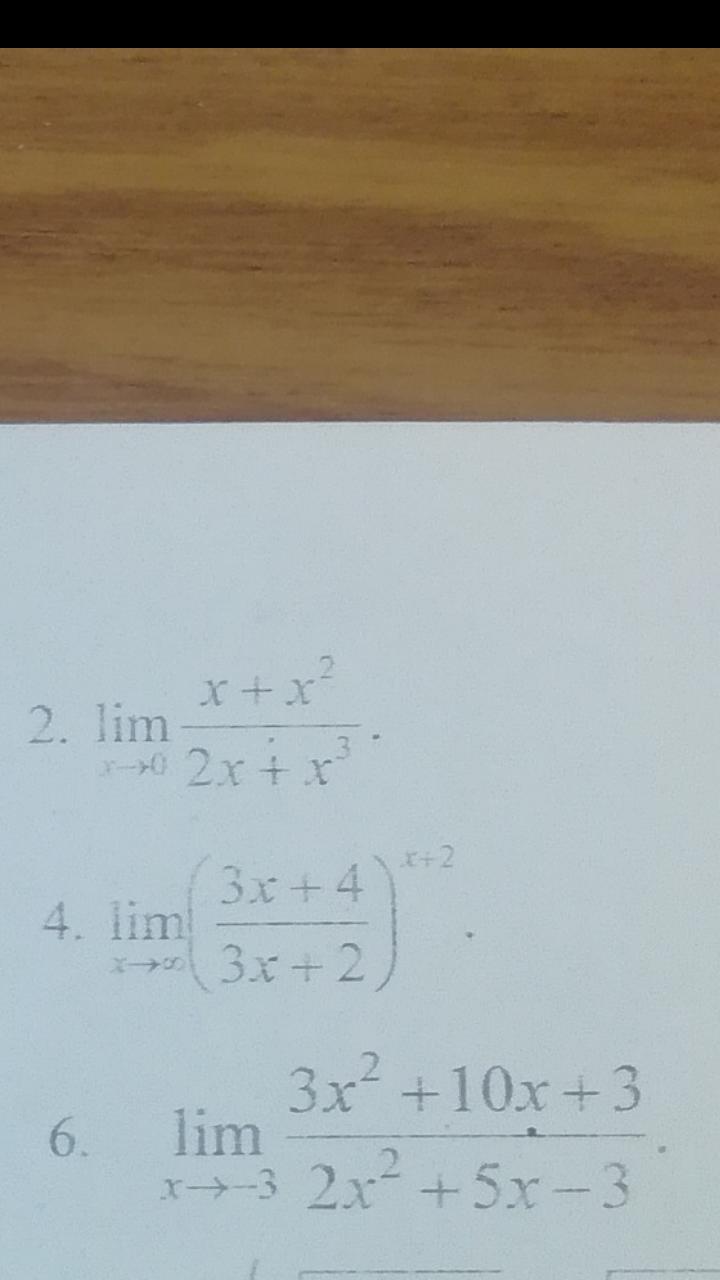
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Алгебра,
автор: Lyrusheva17
Предмет: Українська мова,
автор: valintincibrij
Предмет: Математика,
автор: nnkiwas
Предмет: Математика,
автор: a2eq21
Предмет: Химия,
автор: гной1