Предмет: Математика,
автор: moon814
Упростите выражение и вычислите его значение при х=32, у=1
Приложения:
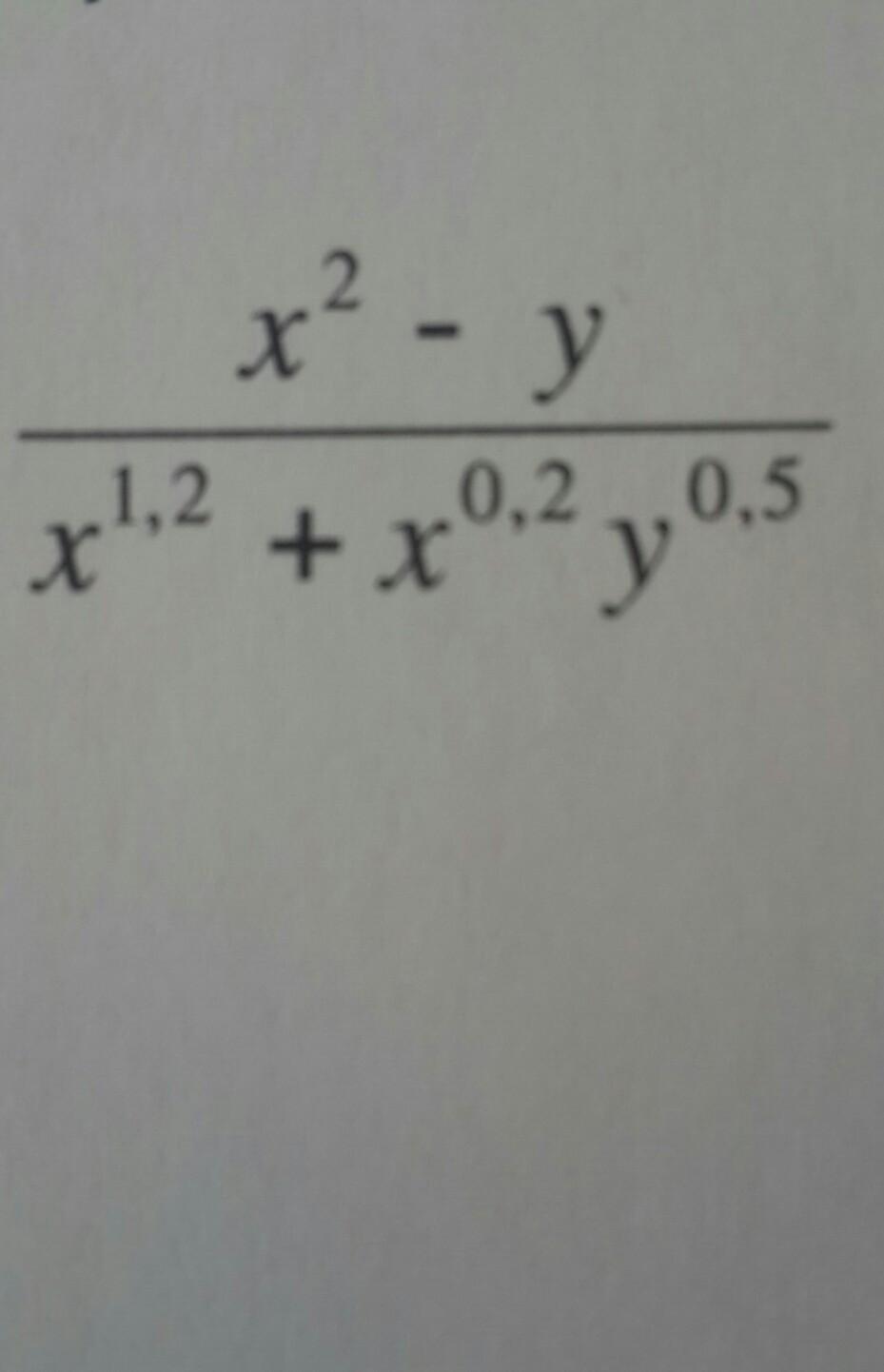
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Українська мова,
автор: pilipchuckaleksej236
Предмет: Математика,
автор: Rinkill
Предмет: Українська мова,
автор: pilipchuckaleksej236
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: zfghdfg