Question

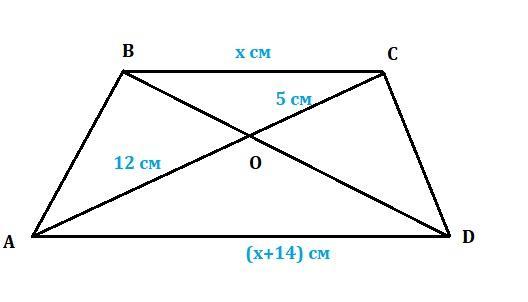
7. Диагонали трапеции ABCD пересекаются в точке 0. Точка пересечения
диагоналей трапеции делит диагональ АС на отрезки длиной 12 см и 5 см.
Найдите основания трапеции AD и BC, если их разность равна 14 см.
Выполните чертеж по условию задачи.​

Answer 1

Ответ:

10 см, 24см

Объяснение:

ABCD - трапеция, O - точка пересечения диагоналей AC и BD, AO = 12 см, CO = 5 см.

Треугольники AOD и COB подобны по 1 признаку подобия:

∠AOD = ∠COB  - как вертикальные.

∠ADO = ∠CBO как накрест лежащие при параллельных AD и BC и секущей BD.

Из подобия треугольников следует подобие соответствующих сторон:

$\dfrac{AD}{BC} =\dfrac{AO}{CO}$

Пусть ВС=х см, тогда AD = (х+14) см

$\dfrac{x+14}{x} =\dfrac{12}{5} \\\\5x+70=12x\\\\7x=70\\\\x=10$

ВС = 10 cм, AD = 10+14 = 24 см