Предмет: Алгебра,
автор: vore4ka
Решите пример подробно, пожалуйста. (тут 2 корня)
Приложения:
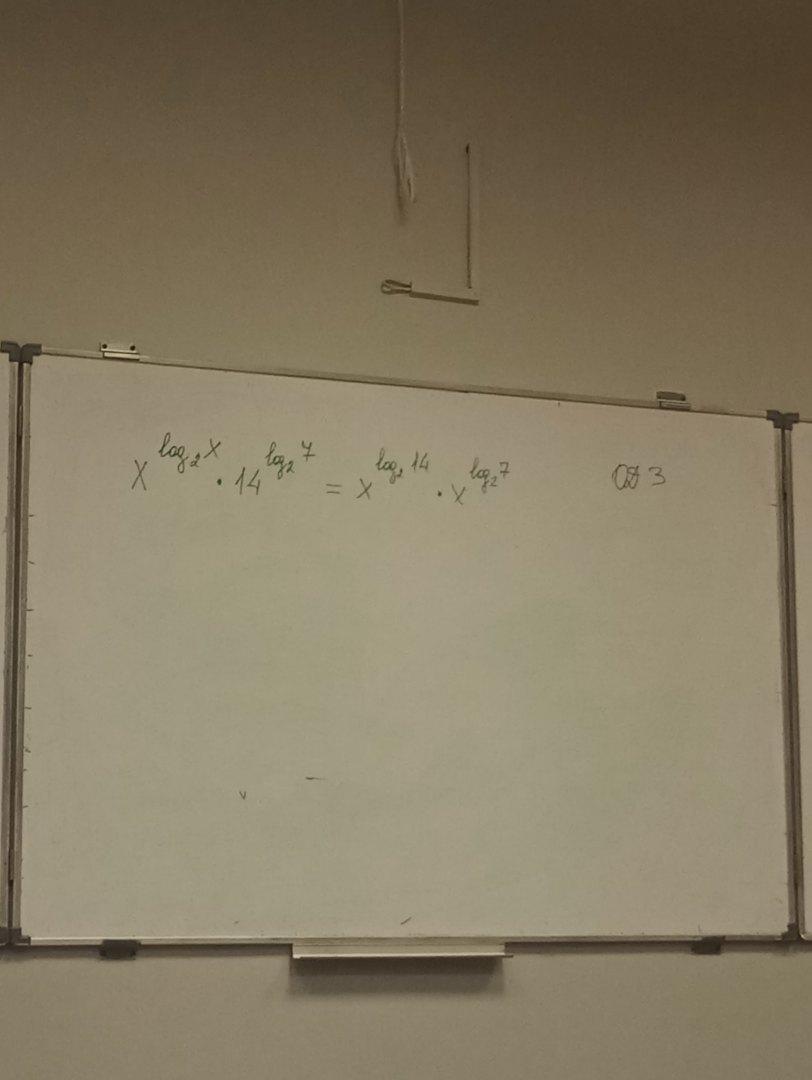
Ответы
Автор ответа:
1
x^(log(2) x) * 14^(log(2) 7) = x^(log(2) 7) * x^(log(2) 14)
ОДЗ x > 0
log (xy) = log x + log y
логарифмируем по основанию 2
log(2) (x^(log(2) x) * 14^(log(2) 7)) = log(2) (x^(log(2) 7) * x^(log(2) 14))
log(2) x^(log(2) x) + log(2) 14^(log(2) 7) = log(2) x^(log(2) 7) + log(2)(x^(log(2) 14)
(log(2) x )*(log(2) x) + (log(2) 14)* (log(2) 7) = log(2) x * (log(2) 7) + (log(2) x)*(log(2) 14)
log(2) x = t
t² - (log(2) 7 + log(2) 14)* t + log(2) 14 * log(2) 7 = 0
D = (log(2) 7 + log(2) 14)²- 4*log(2) 14 * log(2) 7 = (log(2) 14 - log(2) 7)²
t12 = [ (log(2) 14 + log(2) 7) +- (log(2) 14 - log(2) 7)]/2 = log(2) 14 и log(2) 7
1. log(2) x = log(2) 7
x = 7
2. log(2) x = log(2) 14
x = 14
ответ 7 и 14
Похожие вопросы
Предмет: Геометрия,
автор: sofushka152004
Предмет: Английский язык,
автор: grishchenkosveta7
Предмет: Английский язык,
автор: voblayaanastasiya
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: nikita630