Предмет: Математика,
автор: alenaalena200436
Помогите пожалуйста упрастить выражение и пятое доказать ❤️❤️❤️❤️
Приложения:
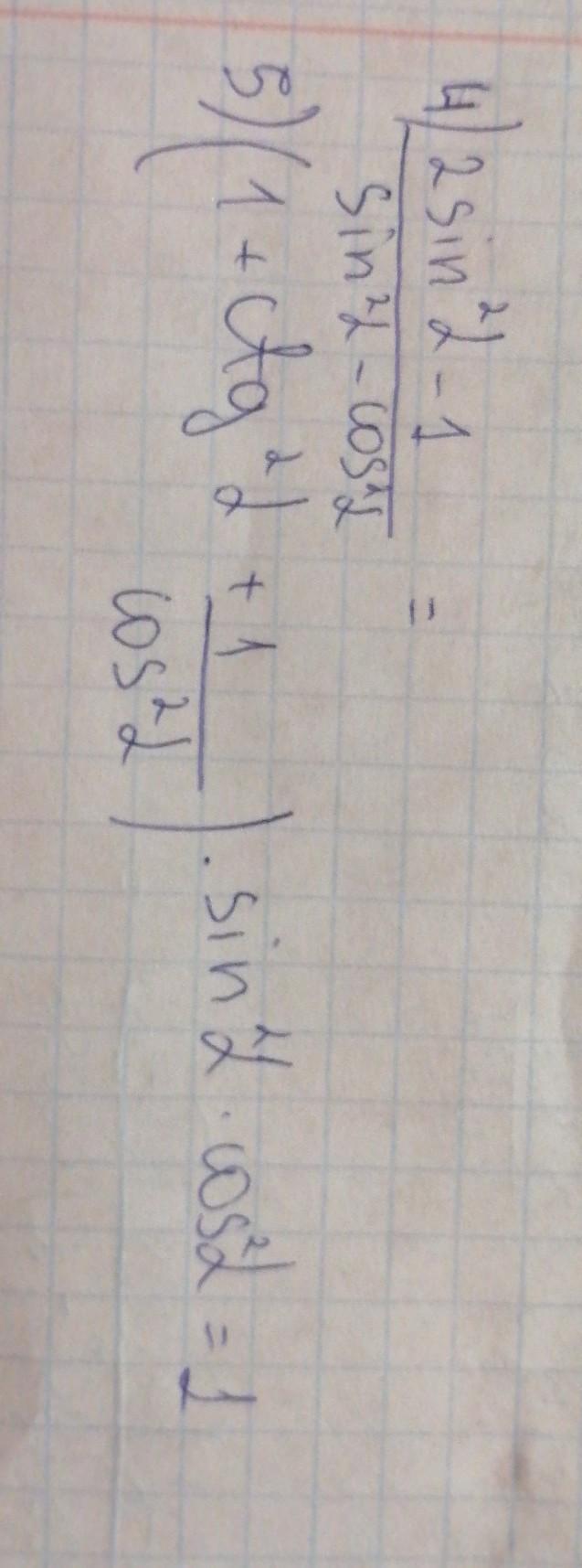
Ответы
Автор ответа:
1
Ответ:
4) Упростим выражение:
5) Докажем тождество:
Похожие вопросы
Предмет: Геометрия,
автор: ychastityy
Предмет: Французский язык,
автор: Аноним
Предмет: Английский язык,
автор: lioncyber58
Предмет: Математика,
автор: лизяком