Предмет: Математика,
автор: EarthColonel
Как перемножать логарифмы с одинаковыми основаниями? Нужно подробное решение этого:
Приложения:
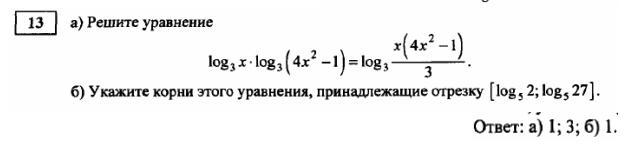
Ответы
Автор ответа:
1
Необходимым условием для существования решение является ; Теперь можно преобразовать:
;
; Отсюда легко найти корни:
; Удовлетворяют найденному в начале промежутку лишь два корня - 1 и 3.
Ответ: 1; 3
Рассмотрим отрезок ; Теперь отвлечемся. Пусть дан отрезок
; Если
; Для нашего отрезка:
; Очевидно, что 3 не входит (5*5*5=125), но 1 подходит.
Ответ: 1.
EarthColonel:
Не понял, как получилась вторая строка после ОДЗ? Эту часть бы подробнее.
log(ab)=log(a)+log(b); log(a/b)=log(a)-log(b)
или имеется в виду не вторая строка. а именно после одз?
ежели так, то просто вынесли общий множитель log(4x^2-1), а log 3 записали как 1
ага, теперь понятно, просто это было очень неочевидно :)
спасибо большое!
спасибо большое!
Похожие вопросы
Предмет: Математика,
автор: nuhkarim2008
Предмет: Математика,
автор: clubanonim193
Предмет: Алгебра,
автор: Jenakosmos
Предмет: Литература,
автор: MoltenGaming