Question

Найдите радиус окружности описанной коло равностороннего треугольника если радиус вписанной в него окружности равен 5 см
Помогите пожаалуйста. Я в 8 классе и мы корни НЕ учили

Answer 1

Радиус описанной окружности в 2 раза больше радиуса вписанной окружности в равносторонний треугольник, значит радиус описанной равен 10 см

Answer 2

Только в равносторонний? И еще разве ест ьаткая теорема?

Answer 3

Именно в равностороннем. Это выведено из формул, там где есть корни, а теоремы не знаю такой.

Answer 4

Что за формулы там где корни? Можете написать а то учительница придраться может. А вообще вы не знаете как как решить эту же задачу через прямоугольный тряугольник

Answer 5

Теория - основа для решения  задач. 
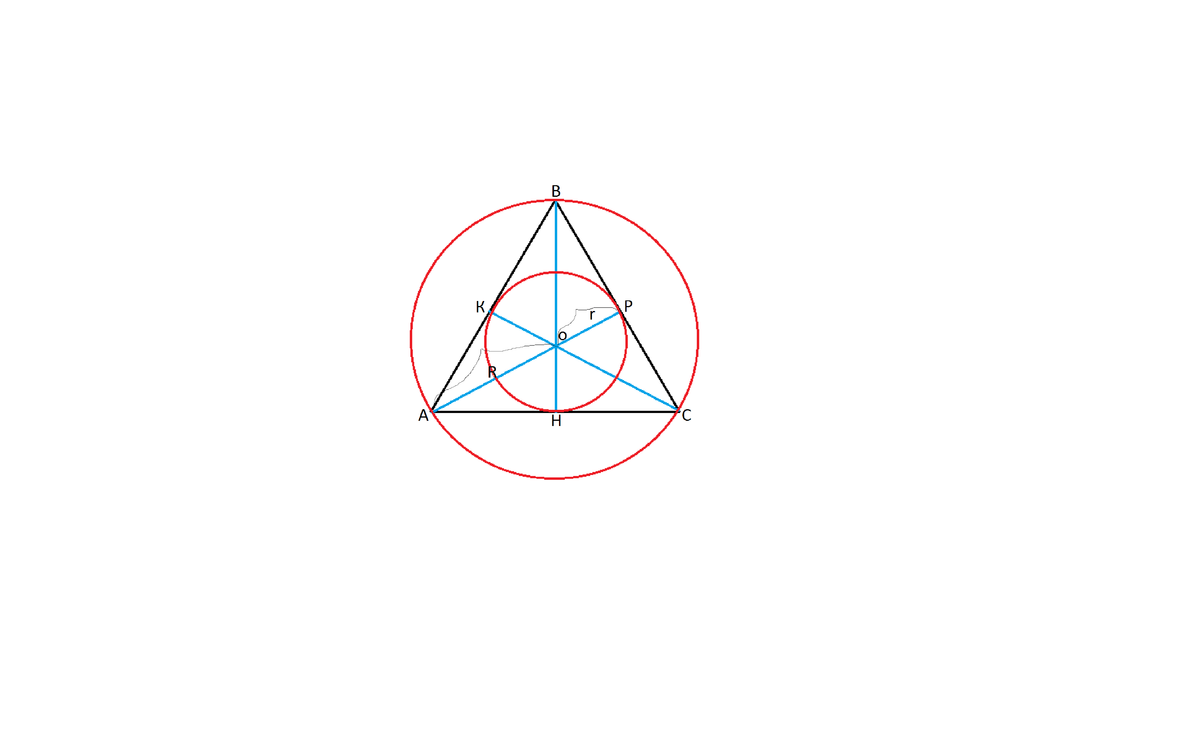
Раз изучаете вписанные и описанные окружности, наверняка уже знаете, что центр вписанной в треугольник окружности находится в точке пересечения его биссектрис. 
Знаете также и то, что
центр описанной окружности - в точке пересечения срединных перпендикуляров, проведенных к каждой из его сторон.  
В равностороннем треугольнике все биссектрисы и высоты пересекаются в одной точке, и эта точка - центр и вписанной, и описанной окружности, так как высота равностороннего треугольника и есть срединный перпендикуляр к стороне. Почему - доказывать не стоит, наверняка знаете.
 О том, что медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1- считая от вершины, Вы уже должны знать. 
Вот на знании всех этих свойств и построено решение задачи. 
Точка пересечения биссектрис треугольника равноудалена от всех его сторон. Расстояние от нее до стороны - радиус вписанной окружности. 
В равностороннем треугольнике это 1/3 медианы -  и это и 1/3 биссектрисы и 1/3 высоты ( три в одном флаконе). 
Радиус описанной вокруг равностороннего треугольника  окружности - расстояние от точки пересечения высот до вершин треугольника, и это расстояние в два раза больше расстояния от точки пересечения биссектрис (высот) до стороны треугольника. 
Итак, радиус описанной вокруг равностороннего треугольника окружности в два раза больше радиуса вписанной в него.
R=2r= 5*2=10 cм
 См. рисунок в качестве иллюстрации.