Предмет: Математика,
автор: kindiuts
Вычислить предел при x стремящимся к 2
Приложения:
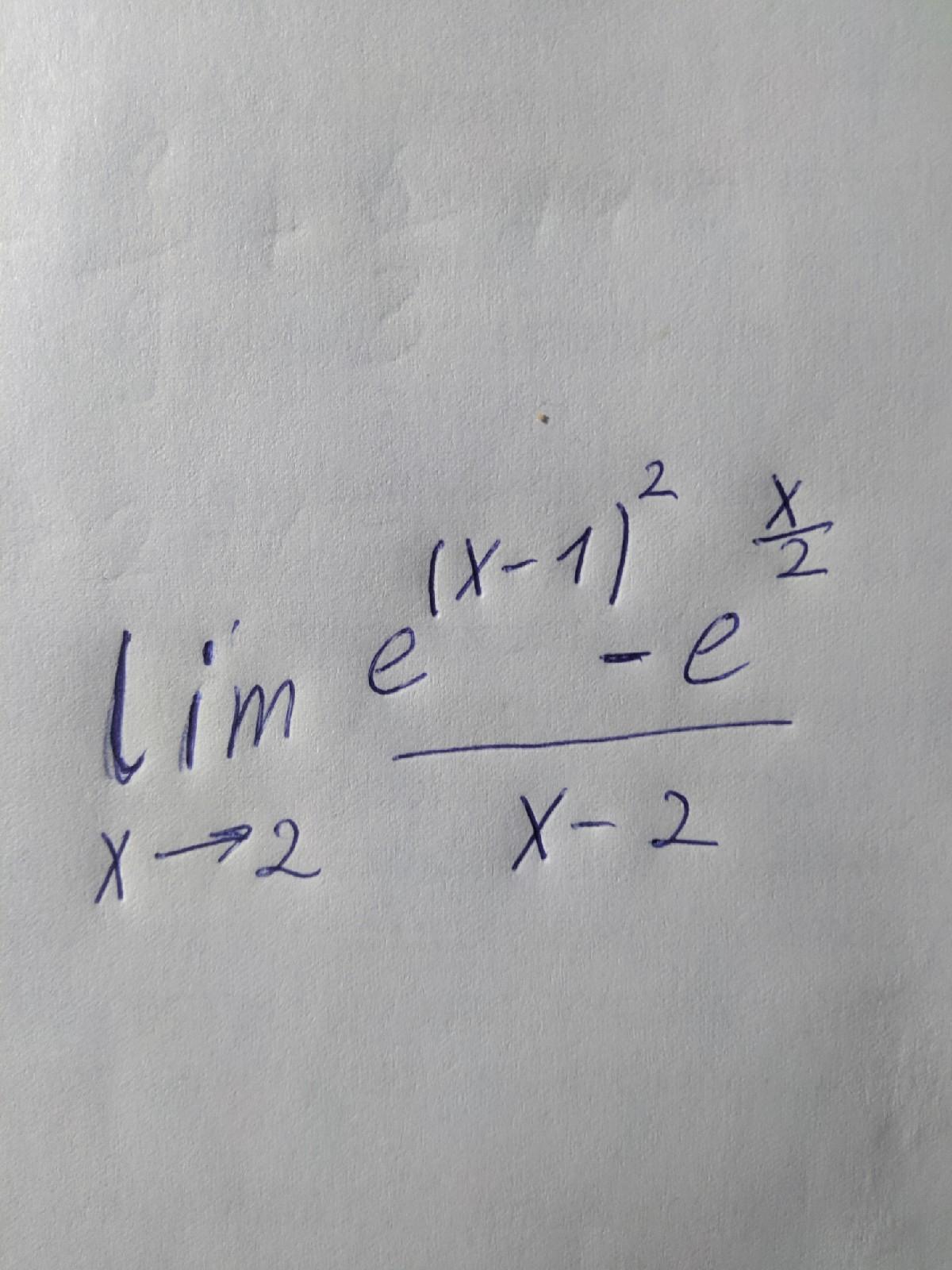
John339:
школьными методами?
или задание вузовское?
вуз
Ответы
Автор ответа:
0
Воспользуемся правилом Лопиталя:
Ответ:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: mouty123
Предмет: Математика,
автор: dimavoychenko02
Предмет: Физика,
автор: Morozovp
Предмет: География,
автор: ксюша3101