Предмет: Математика,
автор: dallon
ПОМОГИТЕ ОЧЕНЬ СРОЧНО!!
Представьте число 2019 в виде a^b+b^a, где a и b - натуральные числа.
Ответы
Автор ответа:
2
Ответ:
2018¹+1²⁰¹⁸=2019
Автор ответа:
2
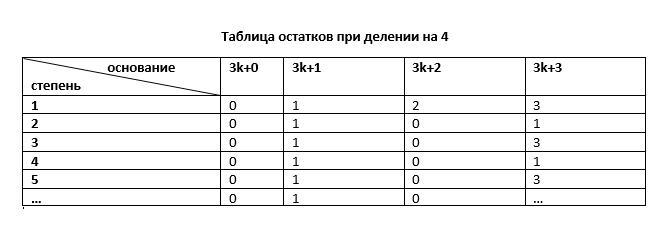
Без нарушения общности будем считать, что остаток от деления на 4 не больше, чем остаток от деления
на 4.
Тогда есть 2 варианта:
. Тогда
или
. Но если
дает остаток 1 или 3 при делении на 4, то никакая степень этого числа не делится на 4. Противоречие с тем, что
.
. Тогда
. Значит имеем решение
В силу симметрии уравнения также имеем решение
Ответ:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: valentinavoinalovich
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: karpenkopolina324
Предмет: Физика,
автор: taninakara
Предмет: Химия,
автор: Gluk1111